Particle Swarm Optimization¶
In this example, we will perform a task that PyRETIS is NOT intended to do. We will optimize a function using a method called particle swarm optimization and the purpose of this example is to illustrate how the PyRETIS library can be used to set up special simulations.
The function we will optimize is the Ackley function which is relatively complex with many local minima as illustrated in the figure below. We will set up our optimization by first creating a new potential and a new engine to do the job for us.
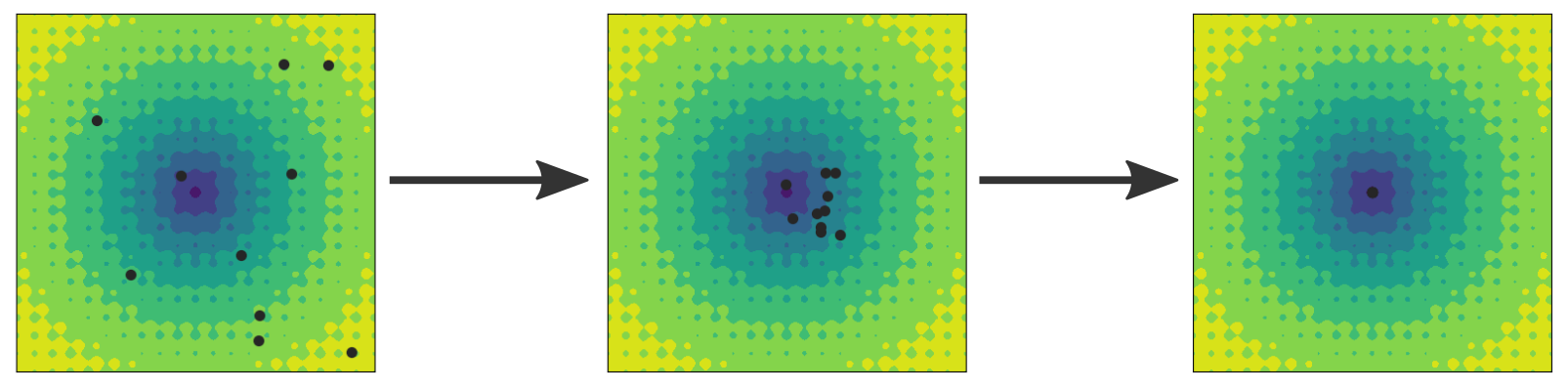
Fig. 38 Illustration of the particle swarm optimization method. The particles (black circles) start in a random initial configuration as shown in the left image and search for the global minimum. All particles keep a record of the smallest value they have seen so far and they communicate this estimate to the other particles. Thus, the current best estimate based on all the particles is known, and the particles are drawn towards this position, but also towards their own best estimate. In the middle image, the positions have been updated and the particles have moved. After some more steps, the particles converge towards the global minimum at (0, 0). However, convergence is not guaranteed.¶
Table of Contents
Creating the Ackley function as a PotentialFunction¶
Here, we will create the function we will optimize as a
PotentialFunction. This can be done by creating a new
file ackley.py and adding the following code:
import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # pylint: disable=unused-import
from pyretis.forcefield import PotentialFunction
TWO_PI = np.pi * 2.0
EXP = np.exp(1)
@np.vectorize
def ackley_potential(x, y): # pylint: disable=invalid-name
"""Evaluate the Ackley function."""
return (-20.0 * np.exp(-0.2*np.sqrt(0.5*(x**2 + y**2))) -
np.exp(0.5 * (np.cos(TWO_PI * x) + np.cos(TWO_PI * y))) +
EXP + 20)
class Ackley(PotentialFunction):
"""A implementation of the Ackley function.
Note that the usage of this potential function differs from
the usual usage for force fields.
"""
def __init__(self):
"""Set up the function."""
super().__init__(dim=2, desc='The Ackley function')
def potential(self, system):
"""Evaluate the potential, note that we return all values."""
xpos = system.particles.pos[:, 0]
ypos = system.particles.pos[:, 1]
pot = ackley_potential(xpos, ypos)
return pot
If you add:
def main():
"""Plot the Ackley function."""
xgrid, ygrid = np.meshgrid(np.linspace(-5, 5, 100),
np.linspace(-5, 5, 100))
zgrid = ackley_potential(xgrid, ygrid)
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax2 = fig.add_subplot(212, projection='3d')
ax1.contourf(xgrid, ygrid, zgrid)
ax2.plot_surface(xgrid, ygrid, zgrid, cmap=plt.get_cmap('viridis'))
plt.show()
if __name__ == '__main__':
main()
you can also plot the potential by running:
python ackley.py
Creating a custom engine for particle swarm optimization¶
Here, we will create a new engine for performing the “dynamics” in the particle swarm optimization. The equations of motion are
For the velocity
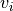 of particle i:
of particle i: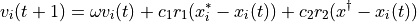
where
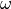 is the co-called inertia weight (a parameter),
is the co-called inertia weight (a parameter), 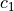 and
and
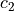 are acceleration coefficients (parameters),
are acceleration coefficients (parameters), 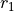 and
and 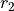 are
random numbers drawn from a uniform distribution between 0 and 1,
are
random numbers drawn from a uniform distribution between 0 and 1, 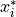 is
particle i’s best estimate of the minimum of the potential and
is
particle i’s best estimate of the minimum of the potential and 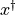 is
the global best estimate.
is
the global best estimate.For the position
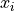 of particle i:
of particle i: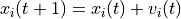
In both equations, 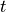 is the current step and
is the current step and 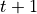 is the next step.
Before updating the positions, the potential energies for the individual particles
are obtained and
is the next step.
Before updating the positions, the potential energies for the individual particles
are obtained and 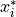 and
and 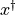 are updated.
are updated.
These equations are similar to the equations used by the MD integrators in
PyRETIS, and the engine can be implemented as a sub-class of the
MDEngine class. Create a new file name psoengine.py
and add the following code:
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
"""A custom engine for particle swarm optimization."""
import numpy as np
from pyretis.engines import MDEngine
class PSOEngine(MDEngine):
"""Perform particle swarm optimization."""
def __init__(self, inertia, accp, accg):
"""Set up the engine.
Parameters
----------
intertia : float
The intertia factor in the velocity equation
of motion.
accp : float
The acceleration for the previous best term. "The congnitive term".
accg : float
The acceleration for the global best term. "The social term".
"""
super().__init__(1, 'Particle Swarm Optimization')
self.inertia = inertia
self.accp = accp
self.accg = accg
self.pbest = None
self.pbest_pot = None
self.gbest = None
self.gbest_pot = None
def integration_step(self, system):
"""Perform one step for the PSO algorithm."""
particles = system.particles
if self.pbest is None:
self.pbest = np.copy(particles.pos)
self.pbest_pot = system.potential()
if self.gbest is None:
pot = system.potential()
idx = np.argmin(pot)
self.gbest = particles.pos[idx]
self.gbest_pot = pot[idx]
rnd1 = np.random.uniform()
rnd2 = np.random.uniform()
particles.vel = (self.inertia * particles.vel +
rnd1 * self.accp * (self.pbest - particles.pos) +
rnd2 * self.accg * (self.gbest - particles.pos))
particles.pos += particles.vel
particles.pos = system.box.pbc_wrap(particles.pos)
pot = system.potential()
# Update global?
idx = np.argmin(pot)
if pot[idx] < self.gbest_pot:
self.gbest_pot = pot[idx]
self.gbest = particles.pos[idx]
# Update for individuals:
idx = np.where(pot < self.pbest_pot)[0]
self.pbest[idx] = np.copy(particles.pos[idx])
self.pbest_pot[idx] = pot[idx]
return self.gbest_pot, self.gbest
Putting it all together and running the optimization¶
We will now create a simulation for performing the optimization. First, we need to import the new potential function and the new engine we have created:
import numpy as np
from pyretis.core import create_box, Particles, System
from pyretis.simulation import Simulation
from pyretis.forcefield import ForceField
from psoengine import PSOEngine
from ackley import Ackley, ackley_potential
We next use this to define a method for setting everything up for us:
NPART = 10
STEPS = 1000
MINX, MAXX = -10, 10
TXT = 'Step: {:5d}: Best: (x, y) = ({:10.3e}, {:10.3e}), pot = {:10.3e}'
def set_up():
"""Just create system and simulation."""
box = create_box(low=[MINX, MINX], high=[MAXX, MAXX],
periodic=[True, True])
print('Created a box:')
print(box)
print('Creating system with {} particles'.format(NPART))
system = System(units='reduced', box=box)
system.particles = Particles(dim=2)
for _ in range(NPART):
pos = np.random.uniform(low=MINX, high=MAXX, size=(1, 2))
system.add_particle(pos)
ffield = ForceField('Single Ackley function',
potential=[Ackley()])
system.forcefield = ffield
print('Force field is:\n{}'.format(system.forcefield))
print('Creating simulation:')
engine = PSOEngine(0.7, 1.5, 1.5)
simulation = Simulation(settings=None, controls={'steps': STEPS})
task_integrate = {'func': engine.integration_step,
'args': [system],
'result': 'gbest', 'first': True}
simulation.add_task(task_integrate)
return simulation, system
Finally, we can make a method to execute the optimization:
def main():
"""Just run the optimization, no plotting."""
simulation, _ = set_up()
for result in simulation.run():
step = result['cycle']['step']
best = result['gbest']
if step % 10 == 0:
print(TXT.format(step, best[1][0], best[1][1], best[0]))
Which is used as follows:
if __name__ == '__main__':
main()
Execute the script a couple of time (save the code above in a
new file, say pso_run.py) and execute it using:
python pso_run.py
Adding plotting and animation¶
If you wish, you can also animate the results/optimization process. First modify the imports as follows:
import numpy as np
from pyretis.core import create_box, Particles, System
from pyretis.simulation import Simulation
from pyretis.forcefield import ForceField
from psoengine import PSOEngine
from ackley import Ackley, ackley_potential
from matplotlib import pyplot as plt
from matplotlib import animation, cm
And add the following methods:
def evaluate_potential_grid():
"""Evaluate the Ackley potential on a grid."""
X, Y = np.meshgrid(np.linspace(MINX, MAXX, 100),
np.linspace(MINX, MAXX, 100))
Z = ackley_potential(X, Y)
return X, Y, Z
def update_animation(frame, system, simulation, scatter):
"""Update animation."""
patches = []
if not simulation.is_finished() and frame > 0:
results = simulation.step()
best = results['gbest']
if frame % 10 == 0:
print(TXT.format(frame, best[1][0], best[1][1], best[0]))
scatter.set_offsets(system.particles.pos)
patches.append(scatter)
return patches
def main_animation():
"""Run the simulation and update for animation."""
simulation, system = set_up()
fig = plt.figure()
ax1 = fig.add_subplot(111, aspect='equal')
ax1.set_xlim((MINX, MAXX))
ax1.set_ylim((MINX, MAXX))
ax1.axes.get_xaxis().set_visible(False)
ax1.axes.get_yaxis().set_visible(False)
X, Y, pot = evaluate_potential_grid()
ax1.contourf(X, Y, pot, cmap=cm.viridis, zorder=1)
scatter = ax1.scatter(system.particles.pos[:, 0],
system.particles.pos[:, 1], marker='o', s=50,
edgecolor='#262626', facecolor='white')
def init():
"""Just return what to re-draw."""
return [scatter]
# This will run the animation/simulation:
anim = animation.FuncAnimation(fig, update_animation,
frames=STEPS+1,
fargs=[system, simulation, scatter],
repeat=False, interval=30, blit=True,
init_func=init)
plt.show()
return anim
if __name__ == '__main__':
main_animation()