RETIS in a 2D potential¶
In this example, you will explore a rare event with the Replica Exchange Transition Interface Sampling (RETIS) algorithm.
In this example, we will implement a new potential for PyRETIS and we will create three new order parameters which we will use to investigate a transition between two stable states in the potential. Using the RETIS algorithm, we will compute the rate constant for the transition between the two stable states.
This example is structured as follows:
Creating the potential function¶
We will consider a relatively simple 2D potential where a single particle is moving.
The potential energy (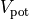 ) is given by
) is given by
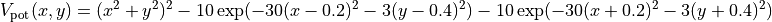
where 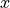 and
and 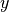 gives the positions.
The potential energy is shown in
Fig. 26 below.
gives the positions.
The potential energy is shown in
Fig. 26 below.
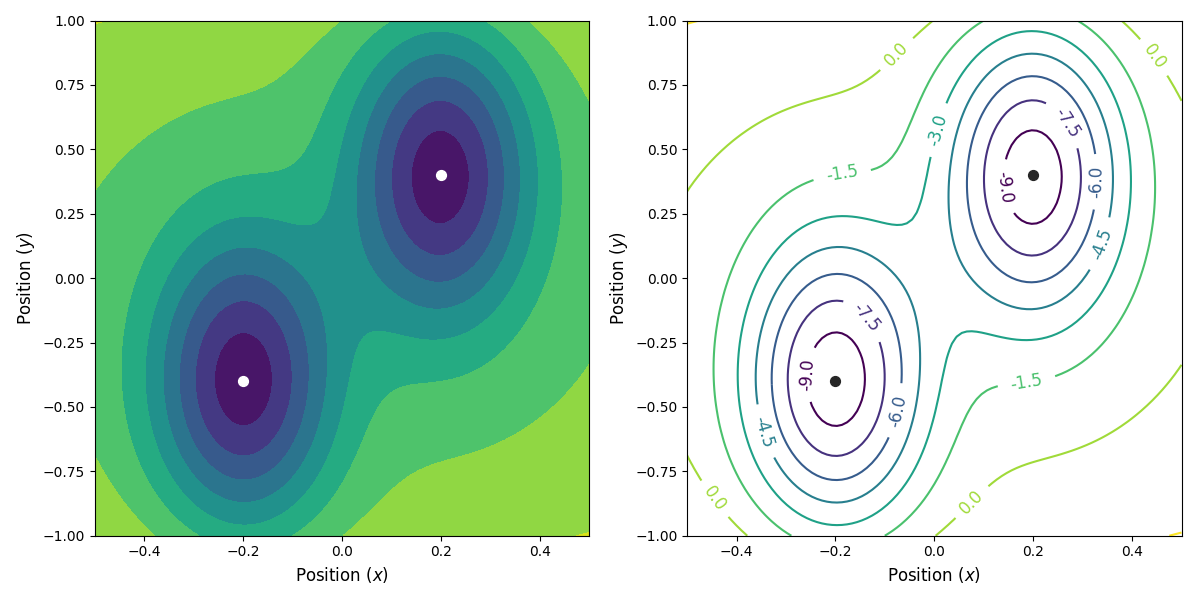
Fig. 26 The potential energy as a function of the position. We have two stable states, at (x, y) = (-0.2, -0.4) and (x, y) = (0.2, 0.4) (indicated with the circles), separated by a saddle point at (x, y) = (0, 0).¶
We begin by creating a new potential function to use with PyRETIS, see the user guide for a short introduction on how custom potential functions can be created. In short, we will now have to define a new class which calculates the potential energy and the corresponding force.
We begin by simply creating a new class for the new potential function. Here, we define the parameters our new potential should accept. We implement the potential slightly more general than the potential given above so that we can change the parameters more easily, if we wish to do so, later. The potential we will be implementing is given by:
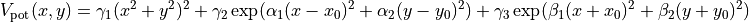
where 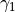 ,
,
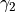 ,
, 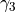 ,
, 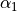 ,
, 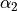 ,
,
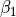 ,
, 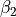 ,
, 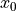 and
and 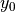 are
potential parameters.
are
potential parameters.
Next, we define a new method as part of our new potential class which will be responsible for calculating the potential energy and a method responsible for calculating the force. Finally, we add a method that will calculate both the potential and the force at the same time. The full Python code for the new potential class can be found below.
Show/hide the new potential class »
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
"""This is a 2D example potential."""
import logging
import numpy as np
from pyretis.forcefield.potential import PotentialFunction
logger = logging.getLogger(__name__) # pylint: disable=invalid-name
logger.addHandler(logging.NullHandler())
class Hyst2D(PotentialFunction):
r"""Hyst2D(PotentialFunction).
This class defines a 2D dimensional potential with two
stable states.
The potential energy (:math:`V_\text{pot}`) is given by
.. math::
V_\text{pot}(x, y) = \gamma_1 (x^2 + y^2)^2 +
\gamma_2 \exp(\alpha_1 (x - x_0)^2 + \alpha_2 (y - y_0)^2) +
\gamma_3 \exp(\beta_1 (x + x_0)^2 + \beta_2(y + y_0)^2)
where :math:`x` and :math:`y` gives the positions and :math:`\gamma_1`,
:math:`\gamma_2`, :math:`\gamma_3`, :math:`\alpha_1`, :math:`\alpha_2`,
:math:`\beta_1`, :math:`\beta_2`, :math:`x_0` and :math:`y_0` are
potential parameters.
Attributes
----------
params : dict
Contains the parameters. The keys are:
* `gamma1`: The :math:`\gamma_1` parameter for the potential.
* `gamma2`: The :math:`\gamma_2` parameter for the potential.
* `gamma3`: The :math:`\gamma_3` parameter for the potential.
* `alpha1`: The :math:`\alpha_1` parameter for the potential.
* `alpha2`: The :math:`\alpha_2` parameter for the potential.
* `beta1`: The :math:`\beta_1` parameter for the potential.
* `beta2`: The :math:`\beta_2` parameter for the potential.
* `x0`: The :math:`x_0` parameter for the potential.
* `y0`: The :math:`y_0` parameter for the potential.
"""
def __init__(self, desc='2D hysteresis'):
"""Set up the potential.
Parameters
----------
a : float, optional
Parameter for the potential.
b : float, optional
Parameter for the potential.
c : float, optional
Parameter for the potential.
desc : string, optional
Description of the force field.
"""
super().__init__(dim=2, desc=desc)
self.params = {'gamma1': 0.0, 'gamma2': 0.0, 'gamma3': 0.0,
'alpha1': 0.0, 'alpha2': 0.0, 'beta1': 0.0,
'beta2': 0.0, 'x0': 0.0, 'y0': 0.0}
def potential(self, system):
"""Evaluate the potential.
Parameters
----------
system : object like `System`
The system we evaluate the potential for. Here, we
make use of the positions only.
Returns
-------
out : float
The potential energy.
"""
x = system.particles.pos[:, 0] # pylint: disable=invalid-name
y = system.particles.pos[:, 1] # pylint: disable=invalid-name
gam1 = self.params['gamma1']
gam2 = self.params['gamma2']
gam3 = self.params['gamma3']
alf1 = self.params['alpha1']
alf2 = self.params['alpha2']
bet1 = self.params['beta1']
bet2 = self.params['beta2']
x_0 = self.params['x0']
y_0 = self.params['y0']
v_pot = (gam1 * (x**2 + y**2)**2 +
gam2 * np.exp(alf1 * (x - x_0)**2 + alf2 * (y - y_0)**2) +
gam3 * np.exp(bet1 * (x + x_0)**2 + bet2 * (y + y_0)**2))
return v_pot.sum()
def force(self, system):
"""Evaluate forces.
Parameters
----------
system : object like `System`
The system we evaluate the potential for. Here, we
make use of the positions only.
Returns
-------
out[0] : numpy.array
The calculated force.
out[1] : numpy.array
The virial, currently not implemented for this potential.
"""
x = system.particles.pos[:, 0] # pylint: disable=invalid-name
y = system.particles.pos[:, 1] # pylint: disable=invalid-name
gam1 = self.params['gamma1']
gam2 = self.params['gamma2']
gam3 = self.params['gamma3']
alf1 = self.params['alpha1']
alf2 = self.params['alpha2']
bet1 = self.params['beta1']
bet2 = self.params['beta2']
x_0 = self.params['x0']
y_0 = self.params['y0']
term = 4.0 * gam1 * (x**2 + y**2)
exp1 = gam2 * np.exp(alf1 * (x - x_0)**2 + alf2 * (y - y_0)**2)
exp2 = gam3 * np.exp(bet1 * (x + x_0)**2 + bet2 * (y + y_0)**2)
forces = np.zeros_like(system.particles.pos)
forces[:, 0] = -(x * term +
2.0 * alf1 * (x - x_0) * exp1 +
2.0 * bet1 * (x + x_0) * exp2)
forces[:, 1] = -(y * term +
2.0 * alf2 * (y - y_0) * exp1 +
2.0 * bet2 * (y + y_0) * exp2)
virial = np.zeros((self.dim, self.dim)) # just return zeros here
return forces, virial
def potential_and_force(self, system):
"""Evaluate the potential and the force.
Parameters
----------
system : object like `System`
The system we evaluate the potential for. Here, we
make use of the positions only.
Returns
-------
out[0] : float
The potential energy as a float.
out[1] : numpy.array
The force as a numpy.array of the same shape as the
positions in `particles.pos`.
out[2] : numpy.array
The virial, currently not implemented for this potential.
"""
virial = np.zeros((self.dim, self.dim)) # just return zeros here
x = system.particles.pos[:, 0] # pylint: disable=invalid-name
y = system.particles.pos[:, 1] # pylint: disable=invalid-name
gam1 = self.params['gamma1']
gam2 = self.params['gamma2']
gam3 = self.params['gamma3']
alf1 = self.params['alpha1']
alf2 = self.params['alpha2']
bet1 = self.params['beta1']
bet2 = self.params['beta2']
x_0 = self.params['x0']
y_0 = self.params['y0']
term0 = (x**2 + y**2)
exp1 = gam2 * np.exp(alf1 * (x - x_0)**2 + alf2 * (y - y_0)**2)
exp2 = gam3 * np.exp(bet1 * (x + x_0)**2 + bet2 * (y + y_0)**2)
v_pot = gam1 * term0**2 + exp1 + exp2
term = 4.0 * gam1 * term0
forces = np.zeros_like(system.particles.pos)
forces[:, 0] = -(x * term +
2.0 * alf1 * (x - x_0) * exp1 +
2.0 * bet1 * (x + x_0) * exp2)
forces[:, 1] = -(y * term +
2.0 * alf2 * (y - y_0) * exp1 +
2.0 * bet2 * (y + y_0) * exp2)
return v_pot.sum(), forces, virial
This new potential function can be included in a PyRETIS simulation by
referencing it in the input file as follows (assuming that it has been
stored in a file named potential.py):
Forcefield settings
-------------------
description = 2D hysteresis
Potential
---------
class = Hyst2D
module = potential.py
parameter gamma1 = 1
parameter gamma2 = -10
parameter gamma3 = -10
parameter alpha1 = -30
parameter alpha2 = -3
parameter beta1 = -30
parameter beta2 = -3
parameter x0 = 0.2
parameter y0 = 0.4
Creating the order parameters¶
In this case, it is not so obvious how to define the order parameter. Three simple possibilities are (see Fig. 27 for an illustration):
- The x coordinate of the particle, where we include the potential energy in order to define the two stable states.
- The y coordinate of the particle, where we include the potential energy in order to define the two stable states.
- The projection of the distance vector from the position of the particle (x, y) to (-0.2, -0.4) onto the straight line between (-0.2, -0.4) and (0.2, 0.4). Here, we also include the potential energy in order to define the two stable states.
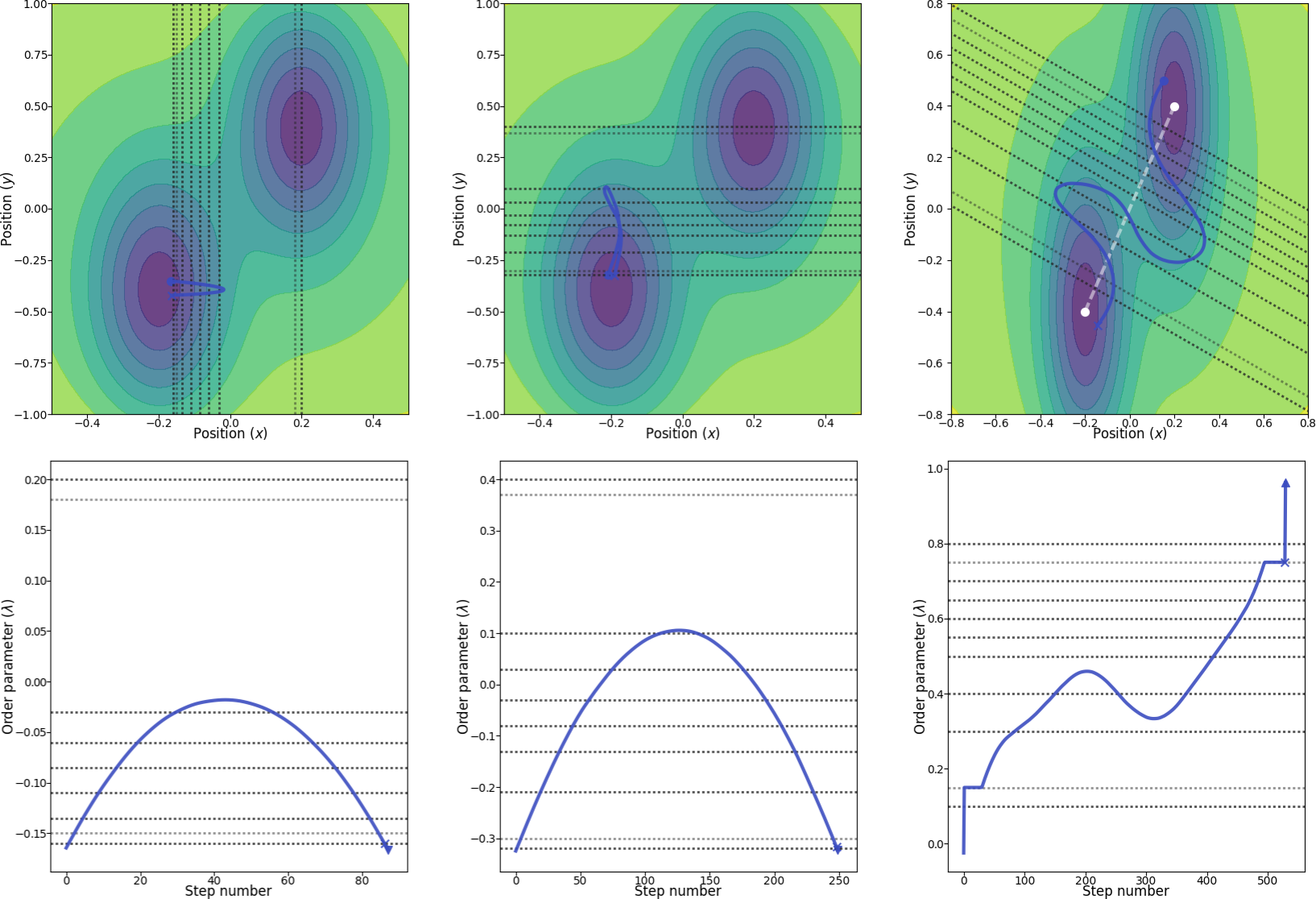
Fig. 27 Illustration of the three different order parameters with location of interfaces (dotted lines). From left to right: using the x position as the order parameter, using the y position as the order parameter and, finally, in the rightmost figure, using a combination of x and y as the order parameter. The white line in the rightmost figure show the line which we project the order parameter onto. The blue paths are valid paths for the final path ensembles and in the bottom row, the corresponding order parameters are shown for these paths. The light dotted interface lines represent the locations where we include the potential energy in the definition of the order parameters. The two marked points (cross and triangle) in the paths in the bottom row show the second last and last points in the paths, respectively. The two marked points (cross and circle) in the paths in the top row show the first and last points in the paths, respectively.¶
Since we include the potential energy in the order parameter definition, we will have to create customized order parameters. There is a short introduction to how the order parameters are implemented in PyRETIS in the user guide and there is also a more lengthy recipe for creating custom order parameters available.
Here, we will first consider the x (or y) order parameter and then the more involved combination.
Creating the x (or y) positional order parameter¶
The order parameter we are now creating will just be the position of the particle with two extra conditions:
- If the position is below a certain value (
inter_a) close to the first interface and if the potential energy is above a certain threshold value (energy_a), then the order parameter will not be allowed to come closer to the first interface. - If the position is closer to the last interface than
a certain value (
inter_b) and if the potential energy is above a certain threshold value (energy_b), then the order parameter will not be allowed to come closer to the last interface.
Thus, in addition to the position of the particle, we need to
consider the 4 additional parameters inter_a, inter_b,
energy_a, energy_b. The Python code for this new
order parameter is given below:
Show/hide the new order parameter »
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
"""The order parameter for the hysteresis example."""
import logging
from pyretis.orderparameter.orderparameter import OrderParameter
logger = logging.getLogger(__name__) # pylint: disable=invalid-name
logger.addHandler(logging.NullHandler())
class OrderX(OrderParameter):
"""A positional order parameter.
Order parameter for the hysteresis example. In addition to using
the position, we also use the energy to tell if we are in states A/B.
Attributes
----------
index : integer
This is the index of the atom which will be used, i.e.
system.particles.pos[index] will be used.
inter_a : float
An interface such that we are in state A for postions < inter_a.
inter_b : float
An interface such that we are in state B for postions > inter_b.
energy_a : float
An energy such that we are in state A for potential energy < energy_a.
energy_b : float
An energy such that we are in state A for potential energy < energy_b.
dim : integer
This is the dimension of the coordinate to use.
0, 1 or 2 for 'x', 'y' or 'z'.
periodic : boolean
This determines if periodic boundaries should be applied to
the position or not.
"""
def __init__(self, index, inter_a, inter_b, energy_a, energy_b,
dim='x', periodic=False):
"""Initialise the order parameter.
Parameters
----------
index : int
This is the index of the atom we will use the position of.
inter_a : float
An interface such that we are in state A for postions < inter_a.
inter_b : float
An interface such that we are in state B for postions > inter_b.
energy_a : float
An energy such that we are in state A for
potential energy < energy_a.
energy_b : float
An energy such that we are in state A for
potential energy < energy_b.
dim : string
This select what dimension we should consider,
it should equal 'x', 'y' or 'z'.
periodic : boolean, optional
This determines if periodic boundary conditions should be
applied to the position.
"""
txt = 'Position of particle {} (dim: {})'.format(index, dim)
super().__init__(description=txt)
self.inter_a = inter_a
self.inter_b = inter_b
self.energy_a = energy_a
self.energy_b = energy_b
self.periodic = periodic
self.index = index
dims = {'x': 0, 'y': 1, 'z': 2}
try:
self.dim = dims[dim]
except KeyError:
msg = 'Unknown dimension {} requested'.format(dim)
logger.critical(msg)
raise
def calculate(self, system):
"""Calculate the order parameter.
Parameters
----------
system : object like :py:class:`.System`
This object is used for the actual calculation, typically
only `system.particles.pos` and/or `system.particles.vel`
will be used. In some cases `system.forcefield` can also be
used to include specific energies for the order parameter.
Returns
-------
out : float
The order parameter.
"""
particles = system.particles
pos = particles.pos[self.index]
lmb = pos[self.dim]
if lmb < self.inter_a:
if particles.vpot > self.energy_a:
lmb = self.inter_a
elif lmb > self.inter_b:
if particles.vpot > self.energy_b:
lmb = self.inter_b
if self.periodic:
return [system.box.pbc_coordinate_dim(lmb, self.dim)]
return [lmb]
This new order parameter can be included in a PyRETIS simulation by
adding the following order parameter section (assuming that the order
parameter is stored in a file order.py):
Orderparameter
--------------
class = OrderX
module = order.py
dim = x
index = 0
periodic = False
inter_a = -0.15
inter_b = 0.18
energy_a = -9.0
energy_b = -9.0
Creating the projection-of-positions order parameter¶
For this order parameter, we will consider the distance from the particle to the stable A state and project the distance vector onto the line joining states A and B. In addition, as in the previously defined order parameters, we will include the energy in the definition of the states.
The Python code for this new order parameter is given below:
Show/hide the new order parameter »
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
"""This file defines the order parameter used for the WCA example."""
import logging
import numpy as np
from pyretis.orderparameter import OrderParameter
logger = logging.getLogger(__name__) # pylint: disable=invalid-name
logger.addHandler(logging.NullHandler())
class OrderXY(OrderParameter):
"""OrderXY(OrderParameter).
This class defines a 2D order parameter such that x + y = constant.
Attributes
----------
index : integer
This selects the particle to use for the order parameter.
inter_a : float
An interface such that we are in state A for postions < inter_a.
inter_b : float
An interface such that we are in state B for postions > inter_b.
energy_a : float
An energy such that we are in state A for potential energy < energy_a.
energy_b : float
An energy such that we are in state A for potential energy < energy_b.
"""
def __init__(self, index, inter_a, inter_b, energy_a, energy_b):
"""Set up the order parameter.
Parameters
----------
index : tuple of ints
This is the indices of the atom we will use the position of.
inter_a : float
An interface such that we are in state A for postions < inter_a.
inter_b : float
An interface such that we are in state B for postions > inter_b.
energy_a : float
An energy such that we are in state A for
potential energy < energy_a.
energy_b : float
An energy such that we are in state A for
potential energy < energy_b.
"""
super().__init__(description='2D->1D projection')
self.index = index
x_1 = 0.2
y_1 = 0.4
x_0 = -0.2
y_0 = -0.4
self.x_0 = x_0
self.y_0 = y_0
self.origin = np.array([x_0, y_0])
self.vec = np.array([x_1 - x_0, y_1 - y_0])
self.vec /= np.sqrt(np.dot(self.vec, self.vec))
self.inter_a = inter_a
self.inter_b = inter_b
self.energy_a = energy_a
self.energy_b = energy_b
def calculate(self, system):
"""Calculate the order parameter.
Here, the order parameter is just the distance between two
particles.
Parameters
----------
system : object like :py:class:`.System`
This object is used for the actual calculation, typically
only `system.particles.pos` and/or `system.particles.vel`
will be used. In some cases `system.forcefield` can also be
used to include specific energies for the order parameter.
Returns
-------
out : float
The order parameter.
"""
pos = system.particles.pos[self.index]
vec = np.array([pos[0] - self.x_0, pos[1] - self.y_0])
proj = np.dot(vec, self.vec)
if proj < self.inter_a:
if system.particles.vpot > self.energy_a:
proj = self.inter_a
elif proj > self.inter_b:
if system.particles.vpot > self.energy_b:
proj = self.inter_b
return [proj]
Note that this order parameter is less general than the previous ones, for instance, we make explicit use of the location of the two minimums. If you are feeling adventurous, please try to add these locations as parameters for the order parameter.
This new order parameter can be included in a PyRETIS simulation by
adding the following order parameter section (assuming that the order
parameter is stored in a file order.py):
Orderparameter
--------------
class = OrderXY
module = orderp.py
index = 0
inter_a = 0.15
inter_b = 0.75
energy_a = -9.0
energy_b = -9.0
Running the RETIS simulation with PyRETIS¶
We have now defined the potential and the order parameters we are going to use and we are ready to run the RETIS simulations.
Running the RETIS simulation using x as the order parameter¶
In order to run the RETIS simulation, the following steps are suggested:
Create a new folder, for instance
2D-hysteresis.Place the order parameter script in this folder and name it
order.py.Download the initial configuration
initial.xyzand place it in the same directory.Create a new sub-directory,
retis-x.Add the following input script
retis-x.rstto theretis-xfolder.Run the simulation using (in the
retis-xfolder):pyretisrun -i retis-x.rst -p
Some examples from the analysis can be found below:
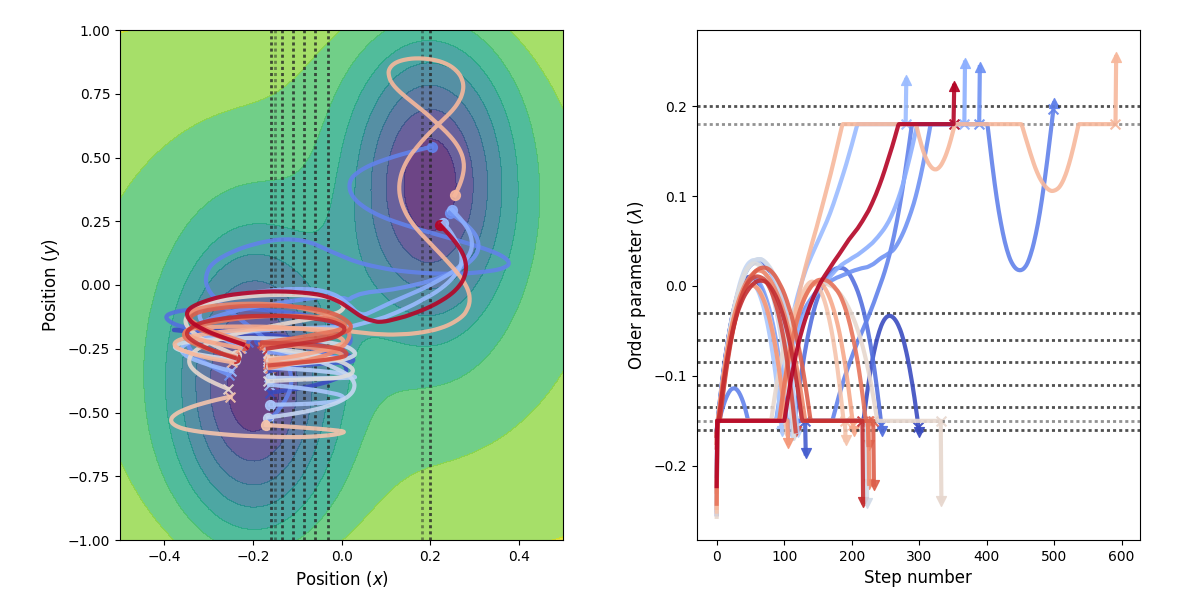
Fig. 28 Example of paths harvested for the RETIS simulation. All paths shown are accepted paths for the last path ensemble.¶
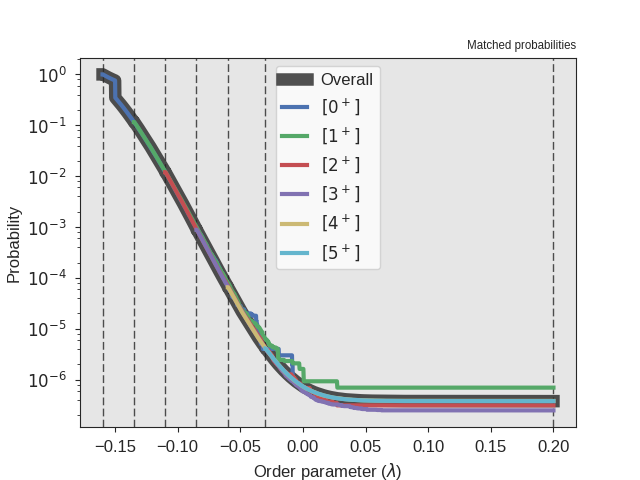
Fig. 29 The crossing probability after 1 000 000 RETIS cycles.
The numerical value is 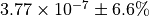 . The
initial flux is
. The
initial flux is 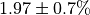 .¶
.¶
Running the RETIS simulation using y as the order parameter¶
In order to run the RETIS simulation, the following steps are suggested:
Create a new folder, for instance
2D-hysteresis.Place the order parameter script in this folder and name it
order.py.Download the initial configuration
initial.xyzand place it in the same directory.Create a new sub-directory,
retis-y.Add the following input script
retis-y.rstto theretis-yfolder.Run the simulation using (in the
retis-yfolder):pyretisrun -i retis-y.rst -p
Some examples from the analysis can be found below:
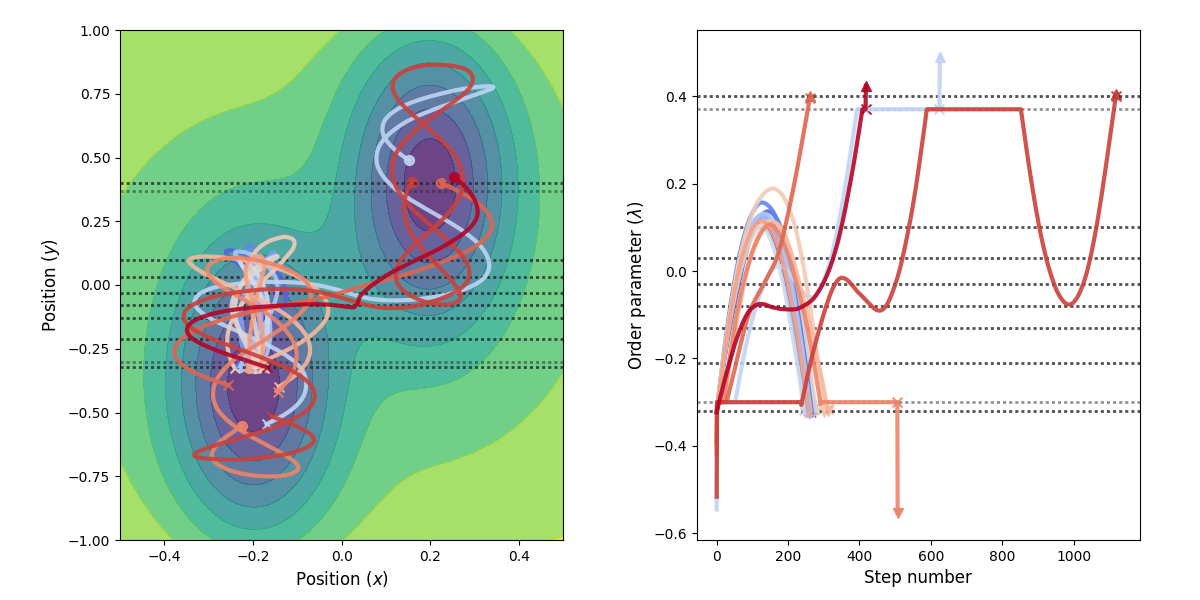
Fig. 30 Example of paths harvested for the RETIS simulation. All paths shown are accepted paths for the last path ensemble.¶
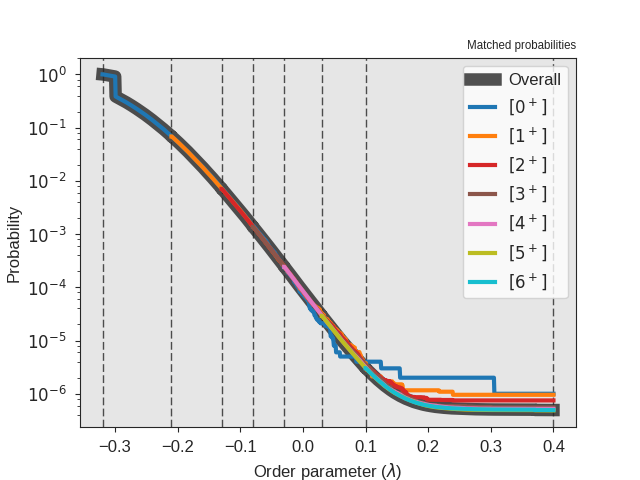
Fig. 31 The crossing probability after 1 000 000 RETIS cycles.
The numerical value is 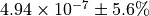 . The
initial flux is
. The
initial flux is 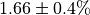 .¶
.¶
Running the RETIS simulation using the projection-of-position as the order parameter¶
In order to run the RETIS simulation, the following steps are suggested:
Create a new folder, for instance
2D-hysteresis.Create a new sub-directory,
retis-xyand move into this directory.Place the order parameter script in this folder and name it
order.py.Download the initial configuration
initial2.xyzand place it in the same directory and rename it toinitial.xyz.Add the following input script
retis-xy.rstto theretis-xyfolder.Run the simulation using (still in the
retis-xyfolder):pyretisrun -i retis-xy.rst -p
Some examples from the analysis can be found below:
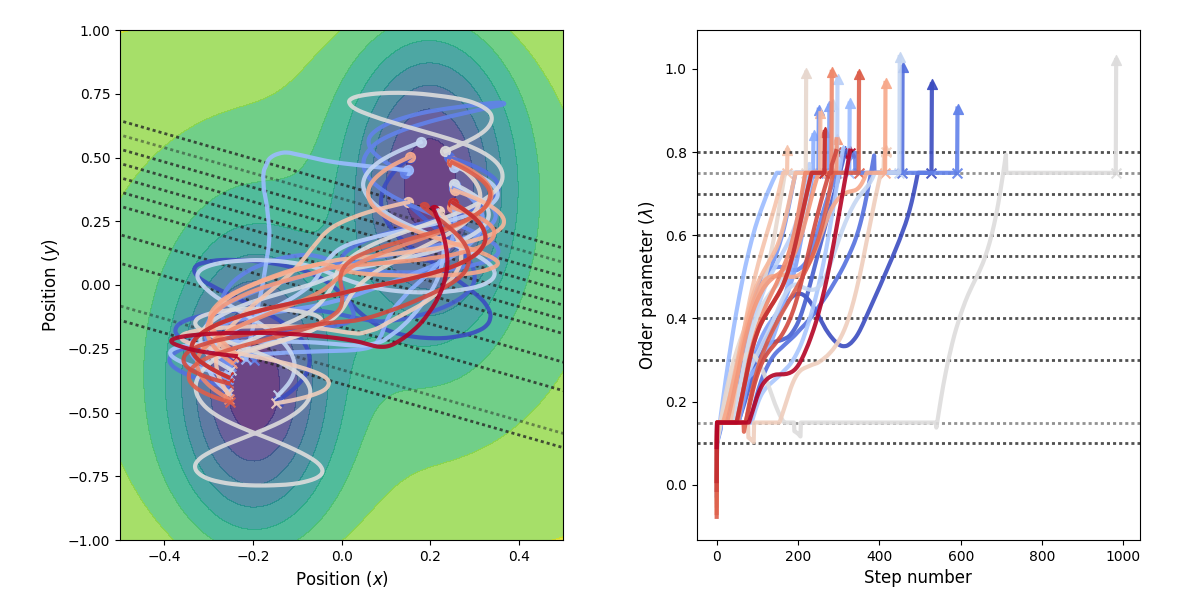
Fig. 32 Example of paths harvested for the RETIS simulation. All paths shown are accepted paths for the last path ensemble.¶
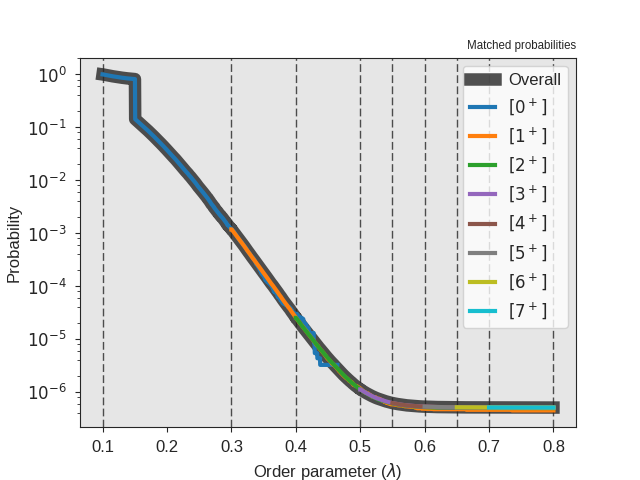
Fig. 33 The crossing probability after 1 000 000 RETIS cycles.
The numerical value is 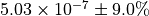 . The
initial flux is
. The
initial flux is 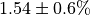 .¶
.¶
Comparing results from the analysis¶
By using the three different order parameters, we obtain different estimates for the rate constant as summarized in the table below.
| Order parameter | Rate constant / 1e-7 | |
|---|---|---|
| Lower bound | Upper bound | |
| x | 7.3 | 8.3 |
| y | 7.7 | 8.6 |
| xy | 7.3 | 8.3 |