Molecular dynamics in PyRETIS with C or FORTRAN¶
In this example, we will implement a Lennard-Jones potential in C or FORTRAN and use this to run a MD simulation with PyRETIS for a simple system. The system we consider is a Lennard-Jones mixture starting for a specific configuration as shown below. After running for some steps (which melt the initial configuration), we reverse the velocities and continue the simulation.

Fig. 36 Snapshots from the MD simulation. To the left, the initial (and final) configuration and to the right, the configuration after running 2000 steps, just before reversing the velocities. The system consist of two types of particles, labeled Ar (colored silver) and Kr (colored purple), which are initially arranged in a particular configuration.¶
Creating a new potential in C or FORTRAN¶
In this example, we will create a new potential function to use with PyRETIS in C or FORTRAN.
As discussed in the introduction to the library, we need to create a new potential class which PyRETIS will make use of. This new potential class will import routines from a C or FORTRAN library and use these routines to do the actual computation of the forces.
We will in the following show how this can be done, both with FORTRAN and with C. Essentially, we are going to complete the following steps:
- We write the code responsible for the evaluation of the force in an external C or FORTRAN library.
- We compile the external code. Here we do one of the following:
- For C, we create a
setup.pywhich is used to compile. - For FORTRAN, make use of a
Makefileand the program f2py.
- For C, we create a
- We write a Python module containing a new
PotentialFunctionsub-class representing the new potential. This class imports the library which we created in steps 1 and 2.
Writing a new potential function with FORTRAN¶
We will now create a potential function writing the external library in FORTRAN. This is done in the following steps:
Step 1. Creating the FORTRAN code¶
The FORTRAN code for evaluating the potential and forces is relative simply and we assume that we are handed positions, velocities, and forces as double precision arrays and that we can directly make use of them.
Show/hide the FORTRAN-code for the potential function »
! Copyright (c) 2023, PyRETIS Development Team.
! Distributed under the LGPLv2.1+ License. See LICENSE for more info.
module ljfortran
implicit none
private
public :: potential, force, potential_and_force
public :: pbc_dist
contains
function pbc_dist(v, box, ibox) result(dist)
! Function to apply periodic boundaries to a given displacement.
!
! Parameters
! ----------
! v : the displacement to pbc-wrap
! box : the box lengths
! ibox : the inverse box lengths, ibox = 1.0 / box
!
! Returns
! -------
! dist : the pbc-wrapped displacement
implicit none
double precision :: dist
double precision, intent(in) :: v, box, ibox
dist = v - nint(v * ibox) * box
end function pbc_dist
subroutine potential(pos, box, ibox, lj3, lj4, offset, rcut2, ptype, n, d, p, vpot)
! Function to evaluate the Lennard-Jones potential
!
! Parameters
! ----------
! pos : positions of the particles
! box : the box lengths
! ibox : the inverse box lengths, ibox = 1.0 / box
! lj3 : Lennard-Jones parameters, 4.0 * epsilonij * sigmaij**12
! lj4 : Lennard-Jones parameters, 4.0 * epsilonij * sigmaij**6
! rcut2 : Squared cut-offs
! offset : Potential energy shift
! ptype : identifier for the particle types
! n : number of particles
! d : dimensionality of the vectors
! p : number of particle types
!
! Returns
! -------
! vpot : the potential energy
implicit none
integer, intent(in) :: n, d, p
double precision, dimension(n, d), target, intent(in) :: pos
double precision, dimension(d), intent(in) :: box, ibox
double precision, dimension(p, p), intent(in) :: lj3, lj4, offset, rcut2
integer, dimension(n), intent(in) :: ptype
double precision, intent(out) :: vpot
double precision :: rsq, r2inv, r6inv, dx, dy, dz
double precision, dimension(:), pointer :: x, y, z
integer :: i, j, itype, jtype
vpot = 0.0D0
x => pos(1:n,1)
y => pos(1:n,2)
z => pos(1:n,3)
do i=1,n-1
itype = ptype(i) + 1
do j=i+1,n
jtype = ptype(j) + 1
dx = x(i) - x(j)
dy = y(i) - y(j)
dz = z(i) - z(j)
dx = pbc_dist(dx, box(1), ibox(1))
dy = pbc_dist(dy, box(2), ibox(2))
dz = pbc_dist(dz, box(3), ibox(3))
rsq = dx*dx + dy*dy + dz*dz
if (rsq < rcut2(jtype, itype)) then
r2inv = 1.0D0 / rsq
r6inv = r2inv**3
vpot = vpot + r6inv * (lj3(jtype, itype) * r6inv - lj4(jtype, itype))
vpot = vpot - offset(jtype, itype)
end if
end do
end do
end subroutine potential
subroutine force(pos, box, ibox, lj1, lj2, rcut2, ptype, n, d, p, forces, virial)
! Function to evaluate the Lennard-Jones force
!
! Parameters
! ----------
! pos : positions of the particles
! box : the box lengths
! ibox : the inverse box lengths, ibox = 1.0 / box
! lj1 : Lennard-Jones parameters, 48.0 * epsilonij * sigmaij**12
! lj2 : Lennard-Jones parameters, 24.0 * epsilonij * sigmaij**6
! rcut2 : Squared cut-offs
! ptype : identifier for the particle types
! n : number of particles
! d : dimensionality of the vectors
! p : number of particle types
!
! Returns
! -------
! forces : the Lennard-Jones forces on the particles
! virial : the virial matrix
implicit none
integer, intent(in) :: n, d, p
double precision, dimension(n, d), target, intent(out) :: forces
double precision, dimension(d, d), intent(out) :: virial
double precision, dimension(n, d), target, intent(in) :: pos
double precision, dimension(d), intent(in) :: box, ibox
double precision, dimension(p, p), intent(in) :: lj1, lj2, rcut2
integer, dimension(n), intent(in) :: ptype
double precision, dimension(:), pointer :: x, y, z, fx, fy, fz
double precision :: rsq, r2inv, r6inv, forcelj, dx, dy, dz
double precision :: forceij_x, forceij_y, forceij_z
integer :: i, j, itype, jtype
x => pos(1:n, 1)
y => pos(1:n,2)
z => pos(1:n,3)
fx => forces(1:n,1)
fy => forces(1:n,2)
fz => forces(1:n,3)
forces = 0.0D0
virial = 0.0D0
do i=1,n-1
itype = ptype(i) + 1
do j=i+1,n
jtype = ptype(j) + 1
dx = x(i) - x(j)
dy = y(i) - y(j)
dz = z(i) - z(j)
dx = pbc_dist(dx, box(1), ibox(1))
dy = pbc_dist(dy, box(2), ibox(2))
dz = pbc_dist(dz, box(3), ibox(3))
rsq = dx*dx + dy*dy + dz*dz
if (rsq < rcut2(jtype, itype)) then
r2inv = 1.0D0 / rsq
r6inv = r2inv*r2inv*r2inv
forcelj = r2inv * r6inv * (lj1(jtype, itype) * r6inv - lj2(jtype, itype))
forceij_x = forcelj * dx
forceij_y = forcelj * dy
forceij_z = forcelj * dz
fx(i) = fx(i) + forceij_x
fy(i) = fy(i) + forceij_y
fz(i) = fz(i) + forceij_z
fx(j) = fx(j) - forceij_x
fy(j) = fy(j) - forceij_y
fz(j) = fz(j) - forceij_z
! accumulate for the virial:
virial(1,1) = virial(1,1) + forceij_x * dx
virial(1,2) = virial(1,2) + forceij_x * dy
virial(1,3) = virial(1,3) + forceij_x * dz
virial(2,1) = virial(2,1) + forceij_y * dx
virial(2,2) = virial(2,2) + forceij_y * dy
virial(2,3) = virial(2,3) + forceij_y * dz
virial(3,1) = virial(3,1) + forceij_z * dx
virial(3,2) = virial(3,2) + forceij_z * dy
virial(3,3) = virial(3,3) + forceij_z * dz
end if
end do
end do
end subroutine force
subroutine potential_and_force(pos, box, ibox, lj1, lj2, lj3, lj4, offset, rcut2, ptype, n, d, p, forces, virial, vpot)
! Function to evaluate the Lennard-Jones force and potential
!
! Parameters
! ----------
! pos : positions of the particles
! box : the box lengths
! ibox : the inverse box lengths, ibox = 1.0 / box
! lj1 : Lennard-Jones parameters, 48.0 * epsilonij * sigmaij**12
! lj2 : Lennard-Jones parameters, 24.0 * epsilonij * sigmaij**6
! lj3 : Lennard-Jones parameters, 4.0 * epsilonij * sigmaij**12
! lj4 : Lennard-Jones parameters, 4.0 * epsilonij * sigmaij**6
! rcut2 : Squared cut-offs
! offset : Potential energy shift
! ptype : identifier for the particle types
! n : number of particles
! d : dimensionality of the vectors
! p : number of particle types
!
! Returns
! -------
! vpot : the potential energy
! forces : the Lennard-Jones forces on the particles
! virial : the virial matrix
implicit none
integer, intent(in) :: n, d, p
double precision, dimension(n, d), target, intent(out) :: forces
double precision, dimension(d, d), intent(out) :: virial
double precision, intent(out) :: vpot
double precision, dimension(n, d), target, intent(in) :: pos
double precision, dimension(d), intent(in) :: ibox, box
double precision, dimension(p, p), intent(in) :: lj1, lj2, lj3, lj4, offset, rcut2
double precision, dimension(:), pointer :: x, y, z, fx, fy, fz
integer, dimension(n), intent(in) :: ptype
double precision :: rsq, r2inv, r6inv, forcelj, dx, dy, dz
double precision :: forceij_x, forceij_y, forceij_z
integer :: i, j, itype, jtype
forces = 0.0D0
virial = 0.0D0
vpot = 0.0D0
x => pos(1:n,1)
y => pos(1:n,2)
z => pos(1:n,3)
fx => forces(1:n,1)
fy => forces(1:n,2)
fz => forces(1:n,3)
do i=1,n-1
itype = ptype(i) + 1
do j=i+1,n
jtype = ptype(j) + 1
dx = x(i) - x(j)
dy = y(i) - y(j)
dz = z(i) - z(j)
dx = pbc_dist(dx, box(1), ibox(1))
dy = pbc_dist(dy, box(2), ibox(2))
dz = pbc_dist(dz, box(3), ibox(3))
rsq = dx*dx + dy*dy + dz*dz
if (rsq < rcut2(jtype, itype)) then
r2inv = 1.0D0 / rsq
r6inv = r2inv*r2inv*r2inv
forcelj = r2inv * r6inv * (lj1(jtype, itype) * r6inv - lj2(jtype, itype))
forceij_x = forcelj * dx
forceij_y = forcelj * dy
forceij_z = forcelj * dz
fx(i) = fx(i) + forceij_x
fy(i) = fy(i) + forceij_y
fz(i) = fz(i) + forceij_z
fx(j) = fx(j) - forceij_x
fy(j) = fy(j) - forceij_y
fz(j) = fz(j) - forceij_z
vpot = vpot + r6inv * (lj3(jtype, itype) * r6inv - lj4(jtype, itype))
vpot = vpot - offset(jtype, itype)
! accumulate for the virial:
virial(1,1) = virial(1,1) + forceij_x * dx
virial(1,2) = virial(1,2) + forceij_x * dy
virial(1,3) = virial(1,3) + forceij_x * dz
virial(2,1) = virial(2,1) + forceij_y * dx
virial(2,2) = virial(2,2) + forceij_y * dy
virial(2,3) = virial(2,3) + forceij_y * dz
virial(3,1) = virial(3,1) + forceij_z * dx
virial(3,2) = virial(3,2) + forceij_z * dy
virial(3,3) = virial(3,3) + forceij_z * dz
end if
end do
end do
end subroutine potential_and_force
end module ljfortran
Step 2. Creating the Makefile and compiling¶
In order to compile the FORTRAN code created in the previous step, we make use of f2py.
Note that in some systems you might actually need to use f2py3
(or, for a specific version: f2py3.7 etc.) if you have several
versions of Python installed on your system. This is to ensure that
the FORTRAN code is compiled with a version that matches the version of
Python you are using. You will then have to modify the F2PY = f2py
setting in the Makefile.
Show/hide the contents of the Makefile »
F2PY = f2py
F2PY_FLAGS = --fcompiler=gfortran
MODULE=ljfortran
all: ${MODULE}.so
${MODULE}.so: ${MODULE}.f90
${F2PY} ${F2PY_FLAGS} -c $< -m ${MODULE}
clean:
find -name \*.so -delete
find -name \*.pyc -delete
find -name __pycache__ -delete
veryclean:
${MAKE} clean
find -name \*energy.dat* -delete
find -name \*thermo.txt* -delete
find -name \*traj.gro* -delete
Note that the FORTRAN compiler is specified using --fcompiler=gfortran
and other choices can be seen by running:
f2py -c --help-fcompiler
Further, the Makefile assumes that the FORTRAN module is named
ljfortran.f90.
Step 3. Creating a new Python class for the potential function¶
For the Python class representing the potential function, we import the module we just compiled and make use of the methods defined in that module.
Show/hide the contents of the new Python class »
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
"""Example of using a Lennard-Jones potential implemented in FORTRAN."""
import sys
from pathlib import Path
import logging
import numpy as np
from pyretis.forcefield.potentials import PairLennardJonesCut
from pyretis.forcefield.potentials.pairpotentials import (
generate_pair_interactions
)
# Just to handle imports of the library:
sys.path.insert(0, Path(__file__).parent.resolve())
logger = logging.getLogger(__name__) # pylint: disable=invalid-name
logger.addHandler(logging.NullHandler())
try:
from ljfortran import ljfortran
except ImportError:
MSG = ('Could not import external FORTRAN library.'
'\nPlease compile with "make"!')
logger.critical(MSG)
raise ImportError(MSG)
__all__ = ['PairLennardJonesCutF']
class PairLennardJonesCutF(PairLennardJonesCut):
r"""class PairLennardJonesCutF(PairLennardJonesCut).
This class implements as simple Lennard-Jones 6-12 potential which
employs a simple cut-off and can be shifted. The potential energy
(:math:`V_\text{pot}`) is defined in the usual way for an
interacting pair of particles a distance :math:`r` apart,
.. math::
V_\text{pot} = 4 \varepsilon \left( x^{12} - x^{6} \right),
where :math:`x = \sigma/r` and :math:`\varepsilon`
and :math:`\sigma` are the potential parameters. The parameters are
stored as attributes of the potential and we store one set for each
kind of pair interaction. Parameters can be generated with a
specific mixing rule by the force field.
Attributes
----------
params : dict
The parameters for the potential. This dict is assumed to
contain parameters for pairs, i.e. for interactions.
_lj : dict of numpy.array
[1] Lennard-Jones parameters used for calculation of the force.
Keys are the pairs (particle types) that may interact.
Calculated as: ``48.0 * epsilon * sigma**12``
[2] Lennard-Jones parameters used for calculation of the force.
Keys are the pairs (particle types) that may interact.
Calculated as: ``24.0 * epsilon * sigma**6``
[3] Lennard-Jones parameters used for calculation of the potential.
Keys are the pairs (particle types) that may interact.
Calculated as: ``4.0 * epsilon * sigma**12``
[4] Lennard-Jones parameters used for calculation of the potential.
Keys are the pairs (particle types) that may interact.
Calculated as: ``4.0 * epsilon * sigma**6``
_offset : numpy.array
Potential values for shifting the potential if requested.
This is the potential evaluated at the cutoff.
_rcut2 : numpy.array
The squared cut-off for each interaction type.
Keys are the pairs (particle types) that may interact.
"""
def __init__(self, dim=3, shift=True, mixing='geometric',
desc='Lennard-Jones pair potential (FORTRAN)'):
"""Set up the Lennard-Jones potential.
Parameters
----------
dim : int
The dimensionality to use.
shift : boolean
Determines if the potential should be shifted or not.
mixing : string
Determines how we should mix potential parameters.
"""
super().__init__(dim=dim, desc=desc, mixing=mixing)
self.ntype = 0
def set_parameters(self, parameters):
"""Update all parameters.
Here, we generate pair interactions, since that is what this
potential actually is using.
Parameters
----------
parameters : dict
The input base parameters.
"""
self.params = {}
pair_param = generate_pair_interactions(parameters, self.mixing)
self.ntype = max(int(np.sqrt(len(pair_param))), 2)
self._lj = {'1': np.zeros((self.ntype, self.ntype)),
'2': np.zeros((self.ntype, self.ntype)),
'3': np.zeros((self.ntype, self.ntype)),
'4': np.zeros((self.ntype, self.ntype))}
self._rcut2 = np.zeros_like(self._lj[1])
self._offset = np.zeros_like(self._lj[1])
for pair in pair_param:
eps_ij = pair_param[pair]['epsilon']
sig_ij = pair_param[pair]['sigma']
rcut = pair_param[pair]['rcut']
self._lj[1][pair] = 48.0 * eps_ij * sig_ij**12
self._lj[2][pair] = 24.0 * eps_ij * sig_ij**6
self._lj[3][pair] = 4.0 * eps_ij * sig_ij**12
self._lj[4][pair] = 4.0 * eps_ij * sig_ij**6
self._rcut2[pair] = rcut**2
vcut = 0.0
if self.shift:
try:
vcut = 4.0 * eps_ij * ((sig_ij / rcut)**12 -
(sig_ij / rcut)**6)
except ZeroDivisionError:
vcut = 0.0
self._offset[pair] = vcut
self.params[pair] = pair_param[pair]
def potential(self, system):
"""Calculate the potential energy for the Lennard-Jones interaction.
Parameters
----------
system : object like :py:class:`.System`
The system we are evaluating the potential in.
Returns
-------
v_pot : float
The potential energy.
"""
particles = system.particles
box = system.box
v_pot = ljfortran.potential(particles.pos,
box.length, box.ilength,
self._lj, self._offset,
self._rcut2, particles.ptype,
particles.npart,
box.dim, self.ntype)
return v_pot
def force(self, system):
"""Calculate the force for the Lennard-Jones interaction.
We also calculate the virial here, since the force
is evaluated.
Parameters
----------
system : object like :py:class:`.System`
The system we are evaluating the force in.
Returns
-------
forces : numpy.array
The forces on the particles.
virial : numpy.array
The virial obtained from the forces.
"""
particles = system.particles
box = system.box
forces, virial = ljfortran.force(particles.pos,
box.length, box.ilength,
self._lj, self._rcut2,
particles.ptype,
particles.npart,
box.dim, self.ntype)
return forces, virial
def potential_and_force(self, system):
"""Calculate potential and force for the Lennard-Jones interaction.
Since the force is evaluated, the virial is also calculated.
Parameters
----------
system : object like :py:class:`.System`
The system we are evaluating the potential and force in.
Note
----
Currently, the virial is only calculated for all the particles.
It is not calculated as a virial per atom. The virial
per atom might be useful to obtain a local pressure or stress,
however, this needs some consideration. Perhaps it's best to
fully implement this as a method of planes or something similar.
Returns
-------
out[0] : float
The potential energy as a float.
out[1] : numpy.array
The force as a numpy.array of the same shape as the
positions in `particles.pos`.
out[2] : numpy.array
The virial, as a symmetric matrix with dimensions
(dim, dim) where dim is given by the box/system dimensions.
"""
particles = system.particles
box = system.box
forces, virial, vpot = ljfortran.potential_and_force(particles.pos,
box.length,
box.ilength,
self._lj,
self._offset,
self._rcut2,
particles.ptype,
particles.npart,
box.dim,
self.ntype)
return vpot, forces, virial
Writing a new potential function with C¶
We will now create a new potential function by writing the external library in C. This is done by the following steps:
Step 1. Creating the C code¶
The C code is more involved, and perhaps cumbersome compared to the FORTRAN code above. We are here explicitly assuming that our system is going to be 3D.
Show/hide the C-code for the potential »
/* Copyright (c) 2023, PyRETIS Development Team.
Distributed under the LGPLv2.1+ License. See LICENSE for more info. */
#define NPY_NO_DEPRECATED_API NPY_1_7_API_VERSION
#include <Python.h>
#include <numpy/arrayobject.h>
#include <math.h>
// Forward function declaration.
static PyObject *potential(PyObject *self, PyObject *args);
static PyObject *force(PyObject *self, PyObject *args);
static PyObject *force_and_pot(PyObject *self, PyObject *args);
// Boilerplate: function list.
static PyMethodDef ljmethods[] = {
{ "potential", potential, METH_VARARGS, "Calculate potential energy."},
{ "force", force, METH_VARARGS, "Calculate force."},
{ "force_and_pot", force_and_pot, METH_VARARGS, "Calculate force and potential energy."},
{ NULL, NULL, 0, NULL } /* Sentinel */
};
static struct PyModuleDef ljc =
{
PyModuleDef_HEAD_INIT,
"ljc",
"Compute Lennard-Jones interactions",
-1,
ljmethods
};
// Boilerplate: Module initialization.
PyMODINIT_FUNC PyInit_ljc(void) {
import_array();
return PyModule_Create(&ljc);
}
static inline npy_float64 pbc_dist(npy_float64 x,
npy_float64 box,
npy_float64 ibox) {
return x - nearbyint(x * ibox) * box;
}
static PyObject *potential(PyObject *self, PyObject *args) {
// Input variables:
npy_int64 npart, dim, ntype;
npy_int64 itype, loc;
PyArrayObject *py_pos, *py_box, *py_ibox, *py_lj3, *py_lj4, *py_rcut2, *py_offset, *py_ptype;
// Internal variables:
npy_float64 dx, dy, dz, rsq, r2inv, r6inv;
npy_int64 i, xi, yi, zi;
npy_int64 j, xj, yj, zj;
// Parse arguments.
if (!PyArg_ParseTuple(args, "O!O!O!O!O!O!O!O!lll",
&PyArray_Type, &py_pos,
&PyArray_Type, &py_box,
&PyArray_Type, &py_ibox,
&PyArray_Type, &py_lj3,
&PyArray_Type, &py_lj4,
&PyArray_Type, &py_offset,
&PyArray_Type, &py_rcut2,
&PyArray_Type, &py_ptype,
&npart, &dim, &ntype)){
return NULL;
}
// Get underlying arrays from numpy arrays.
npy_float64 *pos = (npy_float64*)PyArray_DATA(py_pos);
npy_float64 *box = (npy_float64*)PyArray_DATA(py_box);
npy_float64 *ibox = (npy_float64*)PyArray_DATA(py_ibox);
npy_float64 *lj3 = (npy_float64*)PyArray_DATA(py_lj3);
npy_float64 *lj4 = (npy_float64*)PyArray_DATA(py_lj4);
npy_float64 *rcut2 = (npy_float64*)PyArray_DATA(py_rcut2);
npy_float64 *offset = (npy_float64*)PyArray_DATA(py_offset);
npy_int64 *ptype = (npy_int64*)PyArray_DATA(py_ptype);
npy_float64 vpot = 0.0;
// Calculate potential:
for(i = 0; i < npart-1; i++){
xi = 3*i;
yi = 3*i + 1;
zi = 3*i + 2;
itype = ptype[i];
for (j = i + 1; j < npart; j++){
loc = itype + ntype * ptype[j];
xj = 3*j;
yj = 3*j + 1;
zj = 3*j + 2;
dx = pos[xi] - pos[xj];
dy = pos[yi] - pos[yj];
dz = pos[zi] - pos[zj];
dx = pbc_dist(dx, box[0], ibox[0]);
dy = pbc_dist(dy, box[1], ibox[1]);
dz = pbc_dist(dz, box[2], ibox[2]);
rsq = dx*dx + dy*dy + dz*dz;
if (rsq < rcut2[loc]){
r2inv = 1.0 / rsq;
r6inv = r2inv*r2inv*r2inv;
vpot += r6inv * (lj3[loc] * r6inv - lj4[loc]) - offset[loc];
}
}
}
/* Clean up */
/* Build the output tuple */
PyObject *ret = Py_BuildValue("d", vpot);
return ret;
}
static PyObject *force(PyObject *self, PyObject *args) {
// Input variables:
npy_int64 npart, dim, ntype;
npy_int64 itype, loc;
PyArrayObject *py_pos, *py_box, *py_ibox, *py_force, *py_virial;
PyArrayObject *py_lj1, *py_lj2, *py_rcut2, *py_ptype;
// Internal variables:
npy_float64 dx, dy, dz, rsq, r2inv, r6inv;
npy_float64 forcelj, fx, fy, fz;
npy_int64 i, xi, yi, zi;
npy_int64 j, xj, yj, zj;
// Parse arguments.
if (!PyArg_ParseTuple(args, "O!O!O!O!O!O!O!O!O!lll",
&PyArray_Type, &py_pos,
&PyArray_Type, &py_box,
&PyArray_Type, &py_ibox,
&PyArray_Type, &py_lj1,
&PyArray_Type, &py_lj2,
&PyArray_Type, &py_rcut2,
&PyArray_Type, &py_ptype,
&PyArray_Type, &py_force,
&PyArray_Type, &py_virial,
&npart, &dim, &ntype)){
return NULL;
}
// Get underlying arrays from numpy arrays.
npy_float64 *force = (npy_float64*)PyArray_DATA(py_force);
npy_float64 *virial = (npy_float64*)PyArray_DATA(py_virial);
npy_float64 *pos = (npy_float64*)PyArray_DATA(py_pos);
npy_float64 *box = (npy_float64*)PyArray_DATA(py_box);
npy_float64 *ibox = (npy_float64*)PyArray_DATA(py_ibox);
npy_float64 *lj1 = (npy_float64*)PyArray_DATA(py_lj1);
npy_float64 *lj2 = (npy_float64*)PyArray_DATA(py_lj2);
npy_float64 *rcut2 = (npy_float64*)PyArray_DATA(py_rcut2);
npy_int64 *ptype = (npy_int64*)PyArray_DATA(py_ptype);
// Create array for forces:
//PyObject *ret = PyArray_SimpleNew(dim, test, NPY_DOUBLE);
// Zero virial:
for(i = 0; i < dim*dim; i++) {
virial[i] = 0;
}
// Set all forces to zero.
for(i = 0; i < npart; i++) {
force[3*i] = 0;
force[3*i+1] = 0;
force[3*i+2] = 0;
}
// Calculate forces:
for(i = 0; i < npart-1; i++){
xi = 3*i;
yi = 3*i + 1;
zi = 3*i + 2;
itype = ptype[i];
for (j = i + 1; j < npart; j++){
loc = itype + ntype * ptype[j];
xj = 3*j;
yj = 3*j + 1;
zj = 3*j + 2;
dx = pos[xi] - pos[xj];
dy = pos[yi] - pos[yj];
dz = pos[zi] - pos[zj];
dx = pbc_dist(dx, box[0], ibox[0]);
dy = pbc_dist(dy, box[1], ibox[1]);
dz = pbc_dist(dz, box[2], ibox[2]);
rsq = dx*dx + dy*dy + dz*dz;
if (rsq < rcut2[loc]){
r2inv = 1.0 / rsq;
r6inv = r2inv*r2inv*r2inv;
forcelj = r2inv * r6inv * (lj1[loc] * r6inv - lj2[loc]);
fx = forcelj * dx;
fy = forcelj * dy;
fz = forcelj * dz;
force[xi] += fx;
force[yi] += fy;
force[zi] += fz;
force[xj] -= fx;
force[yj] -= fy;
force[zj] -= fz;
virial[0] += fx*dx;
virial[1] += fx*dy;
virial[2] += fx*dz;
virial[3] += fy*dx;
virial[4] += fy*dy;
virial[5] += fy*dz;
virial[6] += fz*dx;
virial[7] += fz*dy;
virial[8] += fz*dz;
}
}
}
Py_RETURN_NONE;
}
static PyObject *force_and_pot(PyObject *self, PyObject *args) {
// Input variables:
npy_int64 npart, dim, ntype;
npy_int64 itype, loc;
PyArrayObject *py_pos, *py_box, *py_ibox, *py_force, *py_virial;
PyArrayObject *py_lj1, *py_lj2, *py_lj3, *py_lj4, *py_rcut2, *py_offset, *py_ptype;
// Internal variables:
npy_float64 dx, dy, dz, rsq, r2inv, r6inv;
npy_float64 forcelj, fx, fy, fz;
npy_int64 i, xi, yi, zi;
npy_int64 j, xj, yj, zj;
// Parse arguments.
if (!PyArg_ParseTuple(args, "O!O!O!O!O!O!O!O!O!O!O!O!lll",
&PyArray_Type, &py_pos,
&PyArray_Type, &py_box,
&PyArray_Type, &py_ibox,
&PyArray_Type, &py_lj1,
&PyArray_Type, &py_lj2,
&PyArray_Type, &py_lj3,
&PyArray_Type, &py_lj4,
&PyArray_Type, &py_offset,
&PyArray_Type, &py_rcut2,
&PyArray_Type, &py_ptype,
&PyArray_Type, &py_force,
&PyArray_Type, &py_virial,
&npart, &dim, &ntype)){
return NULL;
}
// Get underlying arrays from numpy arrays.
npy_float64 *force = (npy_float64*)PyArray_DATA(py_force);
npy_float64 *virial = (npy_float64*)PyArray_DATA(py_virial);
npy_float64 *pos = (npy_float64*)PyArray_DATA(py_pos);
npy_float64 *box = (npy_float64*)PyArray_DATA(py_box);
npy_float64 *ibox = (npy_float64*)PyArray_DATA(py_ibox);
npy_float64 *lj1 = (npy_float64*)PyArray_DATA(py_lj1);
npy_float64 *lj2 = (npy_float64*)PyArray_DATA(py_lj2);
npy_float64 *lj3 = (npy_float64*)PyArray_DATA(py_lj3);
npy_float64 *lj4 = (npy_float64*)PyArray_DATA(py_lj4);
npy_float64 *offset = (npy_float64*)PyArray_DATA(py_offset);
npy_float64 *rcut2 = (npy_float64*)PyArray_DATA(py_rcut2);
npy_int64 *ptype = (npy_int64*)PyArray_DATA(py_ptype);
npy_float64 vpot = 0.0;
// Create array for forces:
//PyObject *ret = PyArray_SimpleNew(dim, test, NPY_DOUBLE);
// Zero virial:
for(i = 0; i < dim*dim; i++) {
virial[i] = 0;
}
// Set all forces to zero.
for(i = 0; i < npart; i++) {
force[3*i] = 0;
force[3*i+1] = 0;
force[3*i+2] = 0;
}
// Calculate forces:
for(i = 0; i < npart-1; i++){
xi = 3*i;
yi = 3*i + 1;
zi = 3*i + 2;
itype = ptype[i];
for (j = i + 1; j < npart; j++){
loc = itype + ntype * ptype[j];
xj = 3*j;
yj = 3*j + 1;
zj = 3*j + 2;
dx = pos[xi] - pos[xj];
dy = pos[yi] - pos[yj];
dz = pos[zi] - pos[zj];
dx = pbc_dist(dx, box[0], ibox[0]);
dy = pbc_dist(dy, box[1], ibox[1]);
dz = pbc_dist(dz, box[2], ibox[2]);
rsq = dx*dx + dy*dy + dz*dz;
if (rsq < rcut2[loc]){
r2inv = 1.0 / rsq;
r6inv = r2inv*r2inv*r2inv;
forcelj = r2inv * r6inv * (lj1[loc] * r6inv - lj2[loc]);
vpot += r6inv * (lj3[loc] * r6inv - lj4[loc]) - offset[loc];
fx = forcelj * dx;
fy = forcelj * dy;
fz = forcelj * dz;
force[xi] += fx;
force[yi] += fy;
force[zi] += fz;
force[xj] -= fx;
force[yj] -= fy;
force[zj] -= fz;
virial[0] += fx*dx;
virial[1] += fx*dy;
virial[2] += fx*dz;
virial[3] += fy*dx;
virial[4] += fy*dy;
virial[5] += fy*dz;
virial[6] += fz*dx;
virial[7] += fz*dy;
virial[8] += fz*dz;
}
}
}
PyObject *ret = Py_BuildValue("d", vpot);
return ret;
}
As can be seen in the C-code, there is some boilerplate code and we make use of PyArg_ParseTuple in order to parse the parameters to the function.
Step 2. Creating a setup.py file and compiling¶
The C-code can be compiled using a setup.py file.
Show/hide the contents of the setup.py file »
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
"""A script for building the C extension."""
from setuptools import (
setup,
Extension,
)
import numpy as np
LJMODULE = Extension(
'ljc',
sources=['ljc.c'],
extra_compile_args=['-Ofast', '-march=native'],
)
setup(
name='PyRETIS Lennard-Jones c extension',
description='C extension for the Lennard-Jones potential.',
ext_modules=[LJMODULE],
include_dirs=[np.get_include()],
)
The setup.py file is used to compile via the command
python setup.py build_ext --inplace
Here, build_ext is used to tell setup.py to compile the C extension and
the --inplace will put the compiled extensions into the directory you
have the source code in.
Step 3. Creating a new Python class for the potential function¶
The final step is to create a Python class which is making use of the C-code.
Show/hide the contents of the new Python class »
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
"""Example of using a Lennard-Jones potential implemented in C."""
import logging
import sys
from pathlib import Path
import numpy as np
from pyretis.forcefield.potentials import PairLennardJonesCut
from pyretis.forcefield.potentials.pairpotentials import (
generate_pair_interactions
)
# Just to handle imports of the library:
sys.path.insert(0, Path(__file__).parent.resolve())
logger = logging.getLogger(__name__) # pylint: disable=invalid-name
logger.addHandler(logging.NullHandler())
try:
import ljc
except ImportError as exc:
MSG = ('Could not import external C library.'
'\nPlease compile with: "python setup.py build_ext --inplace"')
raise ImportError(MSG) from exc
__all__ = ['PairLennardJonesCutC']
class PairLennardJonesCutC(PairLennardJonesCut):
r"""class PairLennardJonesCutC(PairLennardJonesCut).
This class implements as simple Lennard-Jones 6-12 potential which
employs a simple cut-off and can be shifted. The potential energy
(:math:`V_\text{pot}`) is defined in the usual way for an
interacting pair of particles a distance :math:`r` apart,
.. math::
V_\text{pot} = 4 \varepsilon \left( x^{12} - x^{6} \right),
where :math:`x = \sigma/r` and :math:`\varepsilon`
and :math:`\sigma` are the potential parameters. The parameters are
stored as attributes of the potential and we store one set for each
kind of pair interaction. Parameters can be generated with a
specific mixing rule by the force field.
Attributes
----------
params : dict
The parameters for the potential. This dict is assumed to
contain parameters for pairs, i.e. for interactions.
_lj : dict of numpy.array
[1] Lennard-Jones parameters used for calculation of the force.
Keys are the pairs (particle types) that may interact.
Calculated as: ``48.0 * epsilon * sigma**12``
[2] Lennard-Jones parameters used for calculation of the force.
Keys are the pairs (particle types) that may interact.
Calculated as: ``24.0 * epsilon * sigma**6``
[3] Lennard-Jones parameters used for calculation of the potential.
Keys are the pairs (particle types) that may interact.
Calculated as: ``4.0 * epsilon * sigma**12``
[4] Lennard-Jones parameters used for calculation of the potential.
Keys are the pairs (particle types) that may interact.
Calculated as: ``4.0 * epsilon * sigma**6``
_offset : numpy.array
Potential values for shifting the potential if requested.
This is the potential evaluated at the cutoff.
_rcut2 : numpy.array
The squared cut-off for each interaction type.
Keys are the pairs (particle types) that may interact.
"""
def __init__(self, dim=3, shift=True, mixing='geometric',
desc='Lennard-Jones pair potential (C)'):
"""Set up the Lennard-Jones potential.
Parameters
----------
dim : int
The dimensionality to use.
shift : boolean
Determines if the potential should be shifted or not.
mixing : string
Determines how we should mix potential parameters.
"""
super().__init__(dim=dim, desc=desc, mixing=mixing)
self.shift = shift
self.ntype = 0
def set_parameters(self, parameters):
"""Update all parameters.
Here, we generate pair interactions, since that is what this
potential actually is using.
Parameters
----------
parameters : dict
The input base parameters.
"""
self.params = {}
pair_param = generate_pair_interactions(parameters, self.mixing)
self.ntype = max(int(np.sqrt(len(pair_param))), 2)
self._lj = {'1': np.zeros((self.ntype, self.ntype)),
'2': np.zeros((self.ntype, self.ntype)),
'3': np.zeros((self.ntype, self.ntype)),
'4': np.zeros((self.ntype, self.ntype))}
self._rcut2 = np.zeros_like(self._lj[1])
self._offset = np.zeros_like(self._lj[1])
for pair, value in pair_param.items():
eps_ij = value['epsilon']
sig_ij = value['sigma']
rcut = value['rcut']
self._lj[1][pair] = 48.0 * eps_ij * sig_ij**12
self._lj[2][pair] = 24.0 * eps_ij * sig_ij**6
self._lj[3][pair] = 4.0 * eps_ij * sig_ij**12
self._lj[4][pair] = 4.0 * eps_ij * sig_ij**6
self._rcut2[pair] = rcut**2
vcut = 0.0
if self.shift and rcut**22 > 0:
vcut = 4.0 * eps_ij * ((sig_ij / rcut)**12 -
(sig_ij / rcut)**6)
self._offset[pair] = vcut
self.params[pair] = pair_param[pair]
def potential(self, system):
"""Calculate the potential energy for the Lennard-Jones interaction.
Parameters
----------
system : object like :py:class:`.System`
The system we are evaluating the potential in.
Returns
-------
v_pot : float
The potential energy.
"""
particles = system.particles
box = system.box
v_pot = ljc.potential(particles.pos,
box.length, box.ilength,
self._lj, self._offset,
self._rcut2, particles.ptype,
particles.npart,
box.dim, self.ntype)
return v_pot
def force(self, system):
"""Calculate the force for the Lennard-Jones interaction.
We also calculate the virial here, since the force
is evaluated.
Parameters
----------
system : object like :py:class:`.System`
The system we are evaluating the force in.
Returns
-------
forces : numpy.array
The forces on the particles.
virial : numpy.array
The virial obtained from the forces.
"""
particles = system.particles
box = system.box
forces = np.zeros((particles.npart, box.dim))
virial = np.zeros((box.dim, box.dim))
ljc.force(particles.pos,
box.length, box.ilength,
self._lj, self._rcut2,
particles.ptype,
forces, virial,
particles.npart,
box.dim, self.ntype)
return forces, virial
def potential_and_force(self, system):
"""Calculate potential and force for the Lennard-Jones interaction.
Since the force is evaluated, the virial is also calculated.
Parameters
----------
system : object like :py:class:`.System`
The system we are evaluating the potential and force in.
Note
----
Currently, the virial is only calculated for all the particles.
It is not calculated as a virial per atom. The virial
per atom might be useful to obtain a local pressure or stress,
however, this needs some consideration. Perhaps it's best to
fully implement this as a method of planes or something similar.
Returns
-------
out[0] : float
The potential energy as a float.
out[1] : numpy.array
The force as a numpy.array of the same shape as the
positions in `particles.pos`.
out[2] : numpy.array
The virial, as a symmetric matrix with dimensions
(dim, dim) where dim is given by the box/system dimensions.
"""
particles = system.particles
box = system.box
forces = np.zeros((particles.npart, box.dim))
virial = np.zeros((box.dim, box.dim))
vpot = ljc.force_and_pot(particles.pos,
box.length,
box.ilength,
self._lj,
self._offset,
self._rcut2,
particles.ptype,
forces,
virial,
particles.npart,
box.dim,
self.ntype)
return vpot, forces, virial
Running the MD simulation using the PyRETIS library¶
Below we give a Python script which makes use of the PyRETIS library
to run a MD simulation of 2000 steps in the forward and backward directions.
It will generate a trajectory (named traj.xyz) and display a plot of
the energies (an example is shown in the figure below).
Before running the script you will have to download the initial configuration
initial.gro
and place it in the same directory as the script. Further, the script makes the
following assumptions:
- If you are using FORTRAN (that is if
USE = fortran) the script assumes that there is a folder namedfortranwhich contains the compiled library and the Python script namedljpotentialf.py. - If you are using C (that is if
USE = cpython3) the script assumes that there is a folder namedcpython3which contains the compiled library and the Python script namedljpotentialc.py.
Show/hide the contents of the Python MD script »
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
"""
Example of running a MD NVE simulation.
Here we are running forward and then backward using a potential
written in FORTRAN or C. This can be selected below by the user.
"""
# pylint: disable=invalid-name
import sys
# For plotting:
from matplotlib import pyplot as plt
from matplotlib import gridspec
# PyRETIS imports:
from pyretis.core.units import create_conversion_factors
from pyretis.setup import create_simulation
from pyretis.inout.fileio import FileIO
from pyretis.inout.formats import ThermoTableFormatter
from pyretis.inout.plotting import mpl_set_style
# Define simulation settings:
klass = {'fortran': 'PairLennardJonesCutF',
'cpython3': 'PairLennardJonesCutC'}
module = {'fortran': 'fortran/ljpotentialf.py',
'cpython3': 'cpython3/ljpotentialc.py'}
USE = 'cpython3' # or 'fortran'
settings = {}
settings['simulation'] = {
'task': 'md-nve',
'steps': 2000,
}
settings['system'] = {
'units': 'lj',
'temperature': 2.5,
'dimensions': 3
}
settings['engine'] = {
'class': 'velocityverlet',
'timestep': 0.002
}
settings['output'] = {
'backup': 'overwrite',
'energy-file': 1,
'screen': 10,
'trajectory-file': 1
}
settings['potential'] = [
{'class': klass[USE],
'module': module[USE],
'parameter': {0: {'sigma': 1, 'epsilon': 1, 'factor': 2.5},
1: {'sigma': 1, 'epsilon': 1, 'factor': 2.5}},
'shift': True}
]
settings['particles'] = {
'position': {'input_file': 'initial.gro'},
'velocity': {'generate': 'maxwell', 'momentum': True, 'seed': 0}
}
create_conversion_factors(settings['system']['units'])
simulation_nve = create_simulation(settings)
# Set up extra output:
thermo_file = FileIO('thermo.txt', 'w', ThermoTableFormatter(), backup=False)
thermo_file.open()
store_results = []
# Also create some other outputs:
simulation_nve.set_up_output(settings, progress=False)
# Run the simulation forward:
for result in simulation_nve.run():
stepno = result['cycle']['stepno']
thermo_file.output(stepno, result['thermo'])
result['thermo']['stepno'] = stepno
store_results.append(result['thermo'])
# Run backward:
simulation_nve.ensemble['system'].particles.vel *= -1.0
simulation_nve.extend_cycles(settings['simulation']['steps'] - 1)
for result in simulation_nve.run():
stepno = result['cycle']['stepno']
thermo_file.output(stepno, result['thermo'])
result['thermo']['stepno'] = stepno
store_results.append(result['thermo'])
thermo_file.close()
mpl_set_style() # Load PyRETIS plotting style
step = [res['stepno'] for res in store_results]
pot_e = [res['vpot'] for res in store_results]
kin_e = [res['ekin'] for res in store_results]
tot_e = [res['etot'] for res in store_results]
pressure = [res['press'] for res in store_results]
temp = [res['temp'] for res in store_results]
# Plot some energies:
fig1 = plt.figure()
gs = gridspec.GridSpec(2, 2)
ax1 = fig1.add_subplot(gs[:, 0])
ax1.plot(step, pot_e, label='Potential')
ax1.plot(step, kin_e, label='Kinetic')
ax1.plot(step, tot_e, label='Total')
ax1.set_xlabel('Step no.')
ax1.set_ylabel('Energy per particle')
ax1.legend(loc='center left', prop={'size': 'small'})
ax2 = fig1.add_subplot(gs[0, 1])
ax2.plot(step, temp)
ax2.set_ylabel('Temperature')
ax3 = fig1.add_subplot(gs[1, 1])
ax3.plot(step, pressure)
ax3.set_xlabel('Step no.')
ax3.set_ylabel('Pressure')
fig1.subplots_adjust(bottom=0.12, right=0.95, top=0.95, left=0.12, wspace=0.3)
if 'noplot' not in sys.argv[1:]:
plt.show()
Copy this script and store it in a new Python file,
say md_forward_backward_py. Before running the script, you will have to
set the USE variable in the script to
either USE = fortran or USE = cpython3 to select the external
library to use. After this has been done, you can execute the script as
usual
python md_forward_backward.py
This will run the simulation, and when it is done, it should display
a figure similar to the one given below. Further, you may wish to
inspect the generated trajectory traj.xyz visually.
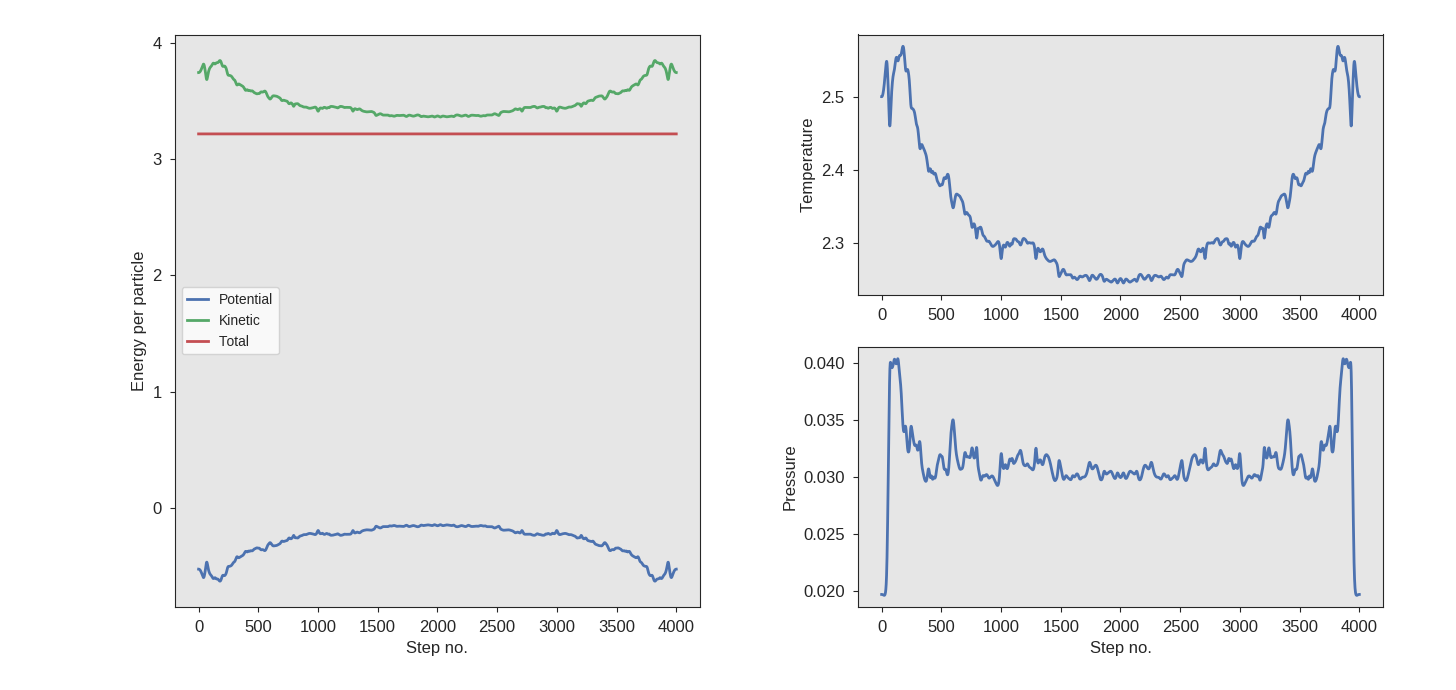
Fig. 37 Energies obtained from the MD run. The velocities were reversed at step 2000.¶