Breaking a bond with RETIS¶
In this example, you will explore bond breaking in a simple model system with the Replica Exchange Transition Interface Sampling (RETIS) algorithm.
The system we consider consist of a simple diatomic bistable molecule immersed in a fluid of purely repulsive particles. This system was actually considered in the article introducing the TIS method, [1] and we will here largely follow this simulation set-up. We refer to the original article for more details.
The potential we use to describe the bond for the diatomic molecule is a double-well potential, similar to the DoubleWellWCA potential implemented in PyRETIS. By tuning the potential parameters, we will consider two cases: one with a high barrier and one with a low barrier.
This example is structured as follows:
The high barrier case¶
For the low barrier case, we will consider a 2D system consisting
of 25 particles and the kinetic energy is scaled so that
the energy of the system is 25 in reduced units. [1] Further, the
number density of the system is set to 0.7,
the barrier height is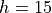 
, the width parameter is 
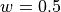and 
.
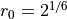Defining the potential functions and the order parameter¶
For this example, we implement both the potential functions and
the order parameter in C. The code can be downloaded as this
zip-archive: high.zip.
In this case, we define the order parameter as the distance between the two atoms in the diatomic molecule.
Running the RETIS simulation¶
The script for running the RETIS simulation is given below. Note that before running the simulation with PyRETIS you will have to compile the C code for the order parameter and the potential functions:
python setup.py build_ext --inplace
The input script given below assumes that the order parameter and the
potential functions are stored in a sub-folder named c-for-python3.
The initial configuration can be downloaded here:
initial-high.xyz.
Show/hide the RETIS input file. »
2D WCA RETIS simulation
=======================
Simulation
----------
task = retis
steps = 1000000
interfaces = [1.24, 1.34, 1.40, 1.46, 1.52, 1.54, 1.64, 1.74]
System
------
units = reduced
dimensions = 2
temperature = 1.0
Box
---
cell = [5.9761430466719681, 5.9761430466719681]
periodic = [True, True]
Engine
------
class = VelocityVerlet
timestep = 0.002
TIS settings
------------
freq = 0.5
maxlength = 20000
aimless = True
allowmaxlength = False
zero_momentum = True
rescale_energy = 25
sigma_v = -1
seed = 0
RETIS settings
--------------
swapfreq = 0.5
relative_shoots = None
nullmoves = True
swapsimul = True
Initial-path
------------
method = kick
Particles
---------
position = {'input_file': '../initial.xyz'}
velocity = {'scale': 25.0}
mass = {'A': 1.0, 'B': 1.0}
name = ['B', 'B', 'A']
ptype = [1, 1, 0]
Forcefield settings
-------------------
description = 2D Double Well + WCA
Potential
---------
class = WCAPotential
module = ../c-for-python3/wcafunctions.py
shift = True
dim = 2
parameter sigma = 1.0
parameter epsilon = 1.0
parameter rcut = 1.122462048309373
parameter idxi = 0
parameter idxj = 1
parameter rzero = 1.122462048309373
parameter height = 15.0
parameter width = 0.5
Orderparameter
--------------
class = WCAOrderParameter
index = (0, 1)
module = ../c-for-python3/wcafunctions.py
Output
------
backup = overwrite
energy-file = 100
order-file = 100
path-file = 1
trajectory-file = 0
The PyRETIS simulation can be executed in the usual way:
pyretisrun -i retis-high.rst -p
Before running the simulation: Ensure that the files and directories (i.e. the initial configuration and the modules referenced) are named correctly with respect to the files you have downloaded for this example.
The low barrier case¶
For the low barrier case, we will consider a 2D system consisting
of 9 particles and the kinetic energy is scaled so that
the energy of the system is 9 in reduced units. [1] Further, the
number density of the system is set to 0.6,
the barrier height is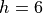 
, the width parameter
is 
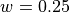and .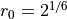
Defining the potential functions and the order parameter¶
For this example, we implement the potential functions in C.
The code can be downloaded as a zip-archive
here: low.zip.
For the order parameter, we include a kinetic energy and potential energy [1] in the definition to ensure the stability of the initial and final states. The Python code for the order parameter can be found below.
Show/hide the order parameter Python script »
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
"""This file defines the order parameter used for the WCA example."""
import logging
import numpy as np
from pyretis.orderparameter import OrderParameter
logger = logging.getLogger(__name__) # pylint: disable=invalid-name
logger.addHandler(logging.NullHandler())
class OrderParameterWCAJCP1(OrderParameter):
"""OrderParameterWCAJCP1(OrderParameter).
This class defines a very simple order parameter which is just
the scalar distance between two particles.
Attributes
----------
index : tuple of integers
These are the indices used for the two particles.
`system.particles.pos[index[0]]` and
`system.particles.pos[index[1]]` will be used.
periodic : boolean
This determines if periodic boundaries should be applied to
the position or not.
"""
def __init__(self, index, periodic=True):
"""Set uå the order parameter.
Parameters
----------
index : tuple of ints
This is the indices of the atom we will use the position of.
periodic : boolean, optional
This determines if periodic boundary conditions should be
applied to the position.
"""
pbc = 'Periodic' if periodic else 'Non-periodic'
txt = '{} distance particles {} and {}'.format(pbc, index[0],
index[1])
super().__init__(description=txt)
self.periodic = periodic
self.index = index
def calculate(self, system):
"""Calculate the order parameter.
Here, the order parameter is just the distance between two
particles.
Parameters
----------
system : object like :py:class:`.System`
This object is used for the actual calculation, typically
only `system.particles.pos` and/or `system.particles.vel`
will be used. In some cases `system.forcefield` can also be
used to include specific energies for the order parameter.
Returns
-------
out : float
The order parameter.
"""
# pylint: disable=invalid-name
particles = system.particles
delta = particles.pos[self.index[1]] - particles.pos[self.index[0]]
if self.periodic:
delta = system.box.pbc_dist_coordinate(delta)
r = np.sqrt(np.dot(delta, delta))
dx = delta
dv = particles.vel[self.index[1]] - particles.vel[self.index[0]]
dxdv = np.dot(dx, dv) / r
m1 = particles.mass[self.index[0]]
m2 = particles.mass[self.index[1]]
m = m1 * m2 / (m1 + m2)
potential_func = system.forcefield.potential[0]
if potential_func is None:
return r
if r < 1.2:
pot = potential_func.potential_well(system) + 0.5 * m * (dxdv)**2
orderp = 1.19
if pot < 1.5:
orderp = 1.18 - (1.5 - pot) / 0.5 * 0.02
elif r > 1.42:
pot = potential_func.potential_well(system) + 0.5 * m * (dxdv)**2
orderp = 1.43
if pot < 5.0:
orderp = 1.44 + (5.0 - pot) / 0.5 * 0.02
else:
orderp = r
return [float(orderp), dxdv]
Running the RETIS simulation¶
The script for running the RETIS simulation is given below. Note that before running the simulation with PyRETIS you will have to compile the C code for the potential
python setup.py build_ext --inplace
and create the script for the order parameter (the input script
given below assumes that the order parameter is stored in a file
orderp.py.
The initial configuration can be downloaded
here: initial-low.xyz.
Show/hide the RETIS input file. »
RETIS simulation 2D WCA, low barrier
====================================
Simulation
----------
task = retis
steps = 1000000
interfaces = [1.2, 1.24, 1.26, 1.32, 1.58]
System
------
units = reduced
dimensions = 2
temperature = 1.0
Box
---
cell = [3.872983346207417, 3.872983346207417]
periodic = [True, True]
Engine
------
class = VelocityVerlet
timestep = 0.002
TIS settings
------------
freq = 0.5
maxlength = 20000
aimless = True
allowmaxlength = False
zero_momentum = True
rescale_energy = 9.0
sigma_v = -1
seed = 0
RETIS settings
--------------
swapfreq = 0.5
relative_shoots = None
nullmoves = True
swapsimul = True
Initial-path
------------
method = kick
Particles
---------
position = {'input_file': '../initial.xyz'}
velocity = {'scale': 9.0}
mass = {'A': 1.0, 'B': 1.0}
name = ['A', 'A', 'A', 'A', 'A', 'A', 'A', 'B', 'B']
ptype = [0, 0, 0, 0, 0, 0, 0, 1, 1]
Forcefield settings
-------------------
description = 2D Double Well + WCA
Potential
---------
class = WCAPotential
module = ../c-for-python3/wcafunctions.py
shift = True
dim = 2
parameter sigma = 1.0
parameter epsilon = 1.0
parameter rcut = 1.122462048309373
parameter idxi = 7
parameter idxj = 8
parameter rzero = 1.122462048309373
parameter height = 6.0
parameter width = 0.25
Orderparameter
--------------
class = OrderParameterWCAJCP1
module = ../c-for-python3/orderp.py
index = (7,8)
periodic = True
Output
------
backup = overwrite
The PyRETIS simulation can be executed in the usual way:
pyretisrun -i retis-low.rst -p
Before running the simulation: Ensure that the files and directories (i.e. the initial configuration and the modules referenced) are named correctly with respect to the files you have downloaded for this example.