RETIS in a 1D potential¶
In this example, you will explore a rare event with the Replica Exchange Transition Interface Sampling (RETIS) algorithm.
We will consider a simple 1D potential where a particle is moving.
The potential is given by
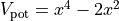 where
where 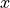 is the position.
By plotting this potential, we see that we have two states
(at
is the position.
By plotting this potential, we see that we have two states
(at 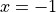 and
and 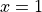 ) separated by a barrier (at
) separated by a barrier (at 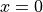 ):
):
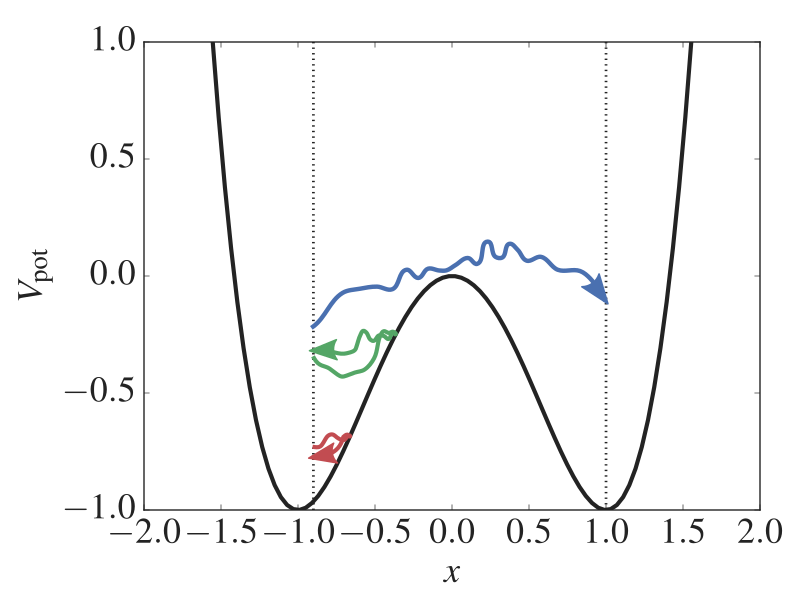
Fig. 22 The potential energy as a function of the position. We have two stable states (at x = -1 and x = 1) separated by a barrier (at x = 0). In addition, three paths are shown. One is reactive while the two others are not able to escape the state at x = -1. Using the RETIS method, we can generate such paths which gives information about the reaction rate and the mechanism. The vertical dotted lines show two RETIS interfaces.¶
Using the RETIS algorithm, we will compute the rate constant for the transition between the two states. This particular problem has been considered before by van Erp [1] [2] and we will here try to reproduce these results.
Creating the PyRETIS input file¶
We will now create the input file for PyRETIS. We will do this section by section in order to explain the different keywords and settings. The full input file is given at the end of this section.
Setting up the simulation task¶
The first thing we will define is the type of simulation we will run. This is done by creating a simulation section.
Here, we are going to do a retis simulation and we will do
20000 steps [2]. Since we will be running a path sampling simulation, we will also need to specify the
positions of the interfaces we will be using.
Retis 1D example
================
Simulation
----------
task = retis
steps = 20000
interfaces = [-0.9, -0.8, -0.7, -0.6, -0.5, -0.4, -0.3, 1.0]
Setting up the system¶
We will now set up the system we are going to consider. Here, we will actually define several PyRETIS input sections:
The system section which defines the units, dimensions and temperature we are considering:
System ------ units = reduced dimensions = 1 temperature = 0.07
The box section, but since we are here just considering a single particle in a 1D potential, we will simply use a 1D box without periodic boundaries:
Box --- periodic = [False]
The particles section which add particles to the system and defines the initial state:
Particles --------- position = {'input_file': 'initial.xyz'} velocity = {'generate': 'maxwell', 'momentum': False, 'seed': 0} mass = {'Ar': 1.0} name = ['Ar'] ptype = [0]
In this case, we will read the initial configuration from a file
initial.xyzand velocities are generated from a Maxwell distribution. Further, we specify the mass, particle type and we label the particle asAr. Note that this does not mean that we are simulating Argon, it is just a label used in the output of trajectories.The force field and potential sections which setup up the 1D double well potential:
Forcefield settings ------------------- description = 1D double well Potential --------- class = DoubleWell a = 1.0 b = 2.0 c = 0.0
Selecting the engine¶
Here, we will make use of a stochastic Langevin engine. We set it up by setting the time step, the friction parameter and whether we are in the high friction limit. The seed given is a seed for the random number generator used by the integrator.
Engine
------
class = Langevin
timestep = 0.002
gamma = 0.3
high_friction = False
seed = 0
TIS specific settings¶
The TIS settings control how the TIS algorithm is carried out.
Here we set that 50 % of the TIS moves should be shooting moves (keyword freq)
and we limit all paths to a maximum length of 20 000 steps.
Further, we select aimless shooting and we tell PyRETIS to not set the
momentum to zero and to not rescale the energy after drawing new random velocities.
We also set allowmaxlength = False which means that for shooting,
we determine stochastically the length of new paths based on the length of
the path we are shooting from. The given seed is a seed for the random number
generator used by the TIS algorithm.
TIS settings
------------
freq = 0.5
maxlength = 20000
aimless = True
allowmaxlength = False
zero_momentum = False
rescale_energy = False
sigma_v = -1
seed = 0
RETIS specific settings¶
The RETIS section controls the RETIS algorithm. Here we request that 50 % of the RETIS moves should be swapping moves, while the remaining 50 % will be TIS moves. We further say that we do not do relative shooting and that we attempt to swap several ensembles at the same time. In case an ensemble is not participating in the swap, a null move (that is just accepting the last accepted path again) is carried out.
RETIS settings
--------------
swapfreq = 0.5
relative_shoots = None
nullmoves = True
swapsimul = True
Initial path settings¶
These settings determine how we find the initial path(s). Here, we ask PyRETIS to generate these using the kick method.
Initial-path settings
---------------------
method = kick
kick-from = initial
Selecting the order parameter¶
For this system, we simply define the order parameter as the position of the single particle we are simulating.
Orderparameter
--------------
class = Position
dim = x
index = 0
periodic = False
Modifying the output¶
In the Output section, we here set the frequency by which PyRETIS will write out information about the trajectories, energies and order parameters.
Output
------
trajectory-file = 100
energy-file = 100
order-file = 100
Show/hide the full input file »
Retis 1D example
================
Simulation
----------
task = retis
steps = 20000
interfaces = [-0.9, -0.8, -0.7, -0.6, -0.5, -0.4, -0.3, 1.0]
System
------
units = reduced
dimensions = 1
temperature = 0.07
Box
---
periodic = [False]
Engine
------
class = Langevin
timestep = 0.002
gamma = 0.3
high_friction = False
seed = 0
TIS settings
------------
freq = 0.5
maxlength = 20000
aimless = True
allowmaxlength = False
zero_momentum = False
rescale_energy = False
sigma_v = -1
seed = 0
RETIS settings
--------------
swapfreq = 0.5
relative_shoots = None
nullmoves = True
swapsimul = True
Initial-path settings
---------------------
method = kick
kick-from = initial
Particles
---------
position = {'input_file': 'initial.xyz'}
velocity = {'generate': 'maxwell',
'momentum': False,
'seed': 0}
mass = {'Ar': 1.0}
name = ['Ar']
ptype = [0]
Forcefield settings
-------------------
description = 1D double well
Potential
---------
class = DoubleWell
a = 1.0
b = 2.0
c = 0.0
Orderparameter
--------------
class = Position
dim = x
index = 0
periodic = False
Output
------
trajectory-file = 100
energy-file = 100
order-file = 100
Running the RETIS simulation¶
We will now run the RETIS simulation. Create a new directory and
place the input file (let’s call it retis.rst) here. Also, download the initial configuration
initial.xyz
and place it in the same folder. The simulation can then be executed using:
pyretisrun -i retis.rst -p
The -p option will display a progress bar for your simulation.
Analysing the results¶
When the simulation has finished, we can analyse the results.
PyRETIS will create a file, out.rst, which you can use for the analysis.
This is a copy of the input retis.rst with some additional settings
for the analysis:
Analysis settings
-----------------
maxordermsd = -1
ngrid = 1001
report = ['latex', 'rst', 'html']
maxblock = 1000
txt-output = 'txt.gz'
blockskip = 1
plot = {'output': 'png', 'plotter': 'mpl', 'style': 'pyretis'}
bins = 100
skipcross = 1000
For a description of these keywords, we refer to the analysis section.
The analysis itself is performed using:
pyretisanalyse -i out.rst
This will produce a new folder, report which contains the
results from the analysis. If you have latex installed, you can
generate a pdf using the file retis_report.tex within the
report folder. An example result for the crossing probability
is shown below.
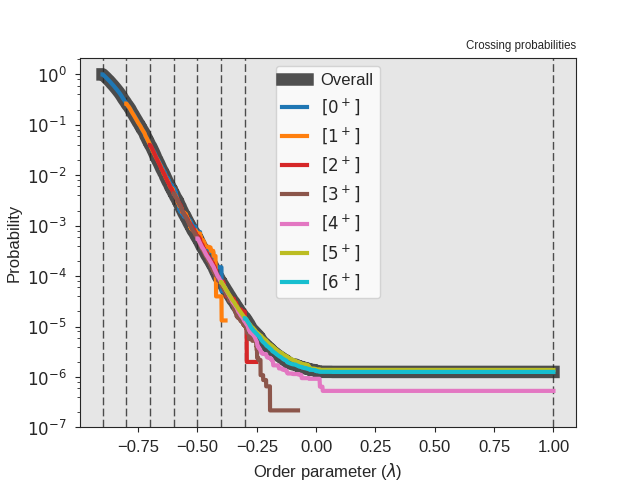
Fig. 23 Sample output from the analysis. This figure shows the crossing probabilities for the individual ensembles and the overall crossing probability.¶
Improving the statistics¶
We can improve the statistics by running a longer simulation. Modify the number of steps, from 20000 to 1000000 and re-run the simulation and the analysis. Below we show an example for the crossing probability after performing the additional steps
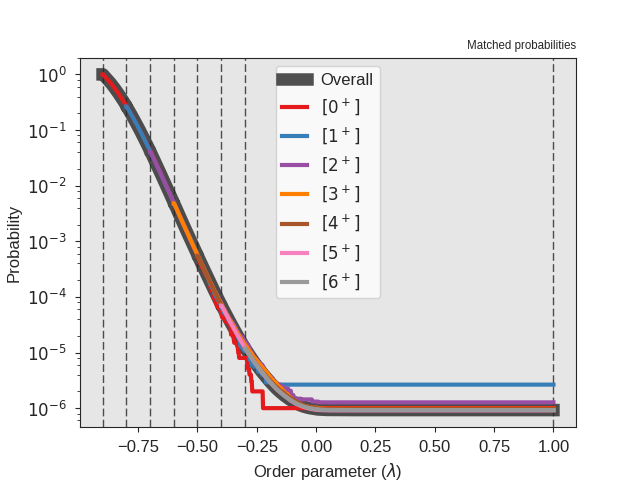
Fig. 24 Sample output from the analysis. This figure shows the crossing probabilities for the individual ensembles and the overall crossing probability after running 1000000 steps.¶
References¶
| [1] | Titus S. Van Erp, Dynamical Rare Event Simulation Techniques for Equilibrium and Nonequilibrium Systems, Advances in Chemical Physics, 151, pp. 27 - 60, 2012, http://dx.doi.org/10.1002/9781118309513.ch2 |
| [2] | (1, 2) https://arxiv.org/abs/1101.0927 |