Using C or FORTRAN¶
In this section, we will show some examples on how C or FORTRAN can be used together with Python and PyRETIS. We show examples on:
- Creating a new Molecular Dynamics engine with C or FORTRAN
- Creating a force field with C or FORTRAN
Creating a new Molecular Dynamics engine with C or FORTRAN¶
In this example, we will create a new molecular dynamics engine using C or FORTRAN. As described in the user guide we have to make a new class and implement a method which performs an integration step. When we now make use of C or FORTRAN in a PyRETIS engine, we essentially just call a method from an external library which we have prepared ourselves (in C or FORTRAN).
In this part, we are here going to create such a library and access it from a piece of Python code. We are going to complete three steps:
- We write the code responsible for the actual integration in an external library.
- We compile the code. Here we do one of the following:
- For C, we create a
setup.pywhich is used to compile. - For FORTRAN, make use of a
Makefileand the program f2py.
- For C, we create a
- We write a Python module containing a new
MDEnginesub-class representing the new engine. This class makes use of the code which we created in steps 1 and 2.
Writing a new engine with FORTRAN¶
We will now create a new engine by writing the external library in FORTRAN. This is done in the following steps:
Step 1. Creating the FORTRAN code¶
The FORTRAN code for creating the new integrator is relatively simple. We can assume that we are handed positions, velocities, and forces as double precision arrays and that we can directly make use of them. Since we need to evaluate the forces during the Velocity Verlet integration, the integration routine is split up in two steps (before/after the evaluation of the forces). The responsibility for updating the forces between these two steps is delegated to the Python script which we will create below.
Show/hide the FORTRAN-code for the engine »
! Copyright (c) 2023, PyRETIS Development Team.
! Distributed under the LGPLv2.1+ License. See LICENSE for more info.
module vvintegrator
implicit none
private
public :: step1, step2
contains
subroutine step1(pos, vel, force, imass, delta_t, half_delta_t, n, d, dpos, dvel)
! Part 1 of the velocity verlet update.
implicit none
integer, intent(in) :: n, d
double precision, dimension(n, d), intent(in) :: pos, vel, force
double precision, dimension(n), intent(in) :: imass
double precision, intent(in) :: delta_t, half_delta_t
double precision, dimension(n, d), intent(out) :: dvel, dpos
integer :: i
dvel = 0.0D0
dpos = 0.0D0
do i=1,d
dvel(:,i) = vel(:,i) + half_delta_t * force(:,i) * imass(:)
dpos(:,i) = pos(:,i) + delta_t * dvel(:,i)
end do
end subroutine step1
subroutine step2(vel, force, imass, half_delta_t, n, d, dvel)
! Part 2 of the velocity verlet update.
implicit none
integer, intent(in) :: n, d
double precision, dimension(n, d), intent(in) :: vel, force
double precision, dimension(n), intent(in) :: imass
double precision, intent(in) :: half_delta_t
double precision, dimension(n, d), intent(out) :: dvel
integer :: i
dvel = 0.0D0
do i=1,d
dvel(:,i) = vel(:,i) + half_delta_t * force(:,i) * imass(:)
end do
end subroutine step2
end module vvintegrator
Step 2. Creating the Makefile and compiling¶
In order to compile the FORTRAN code created in the previous step, we make use of f2py.
Note that
in some cases you might actually need to use f2py3 (or, for a specific version: f2py3.7 etc.)
to compile the FORTRAN code so that it can be used with the version of Python you are using to run
this example. You will then have to modify the F2PY = f2py setting in the Makefile
Show/hide the contents of the Makefile »
F2PY = f2py
F2PY_FLAGS = --fcompiler=gfortran
MODULE=vvintegrator
all: ${MODULE}.so
${MODULE}.so: ${MODULE}.f90
${F2PY} ${F2PY_FLAGS} -c $< -m ${MODULE}
clean:
find -name \*.so -delete
find -name \*.pyc -delete
find -name __pycache__ -delete
-rm thermo.txt*
-rm traj.xyz*
-rm energy.txt*
-rm pyretis.log*
-rm pyretis.restart*
-rm out.rst*
Note that the FORTRAN compiler is specified using --fcompiler=gfortran
and other choices can be seen by running:
f2py -c --help-fcompiler
Further, the Makefile assumes that the FORTRAN module is named
vvintegrator.f90.
Step 3. Creating a new Python class for the engine¶
For the Python class representing the engine, we just import the
module we just compiled and make use of the two methods defined within
that module. Note that we here make an explicit call to system.potential_and_force()
so that forces are updated between the two “steps” of the Velocity Verlet integration.
Show/hide the contents of the Python class »
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
"""Example of using a integration routine implemented in FORTRAN."""
import logging
import os
import sys
from pyretis.engines import MDEngine
logger = logging.getLogger(__name__) # pylint: disable=invalid-name
logger.addHandler(logging.NullHandler())
sys.path.insert(0, os.path.abspath(os.path.dirname(__file__)))
try:
from vvintegrator import vvintegrator
except ImportError:
MSG = ('Could not import external FORTRAN library.'
'\nPlease compile with "make"!')
logger.critical(MSG)
raise ImportError(MSG)
__all__ = ['VelocityVerletF']
class VelocityVerletF(MDEngine):
"""VelocityVerletF(MDEngine).
This class defines the Velocity Verlet integrator.
Attributes
----------
timestep : float
The time step.
half_timestep : float
The half of the timestep.
desc : string
Description of the integrator.
"""
def __init__(self, timestep,
desc='The velocity verlet integrator (FORTRAN)'):
"""Set up the Velocity Verlet integrator.
Parameters
----------
timestep : float
The time step.
desc : string
Description of the integrator.
"""
super().__init__(timestep, desc, dynamics='NVE')
self.half_timestep = self.timestep * 0.5
def integration_step(self, system):
"""Velocity Verlet integration, one time step.
Parameters
----------
system : object like :py:class:`.System`
The system to integrate/act on. Assumed to have a particle
list in `system.particles`.
Returns
-------
out : None
Does not return anything, but alters the state of the given
`system`.
"""
particles = system.particles
particles.pos, particles.vel = vvintegrator.step1(
particles.pos,
particles.vel,
particles.force,
particles.imass,
self.timestep,
self.half_timestep
)
system.potential_and_force()
particles.vel = vvintegrator.step2(
particles.vel,
particles.force,
particles.imass,
self.half_timestep
)
You can now use the new integrator, for instance by adding the following engine section to the input file:
Engine
------
class = VelocityVerletF
timestep = 0.002
module = vvintegratorf.py
Writing a new engine with C¶
We will now create a new engine by writing the external library in C. This is done in the following steps:
Step 1. Creating the C code¶
The C code is more involved, and perhaps cumbersome compared to the FORTRAN code above. We are here explicitly assuming that our system is going to be 3D and we split the Velocity Verlet integration into two steps as in the FORTRAN code.
Show/hide the C-code for the engine »
/* Copyright (c) 2023, PyRETIS Development Team.
Distributed under the LGPLv2.1+ License. See LICENSE for more info. */
#define NPY_NO_DEPRECATED_API NPY_1_7_API_VERSION
#include <Python.h>
#include <numpy/arrayobject.h>
#include <math.h>
// Forward function declaration.
static PyObject *step1(PyObject *self, PyObject *args);
static PyObject *step2(PyObject *self, PyObject *args);
// Boilerplate: function list.
static PyMethodDef vvmethods[] = {
{ "step1", step1, METH_VARARGS, "Velocity Verlet - update positions and velocity"},
{ "step2", step2, METH_VARARGS, "Velocity Verlet - update velocity"},
{ NULL, NULL, 0, NULL } /* Sentinel */
};
static struct PyModuleDef vvintegrator =
{
PyModuleDef_HEAD_INIT,
"vvintegrator",
"Velocity Verlet Integrator",
-1,
vvmethods
};
// Boilerplate: Module initialization.
PyMODINIT_FUNC PyInit_vvintegrator(void) {
import_array();
return PyModule_Create(&vvintegrator);
}
static PyObject *step1(PyObject *self, PyObject *args) {
// Input variables:
npy_int64 npart, dim;
npy_float64 delta_t, half_delta_t;
PyArrayObject *py_pos, *py_vel, *py_force, *py_imass;
// Internal variables:
npy_int64 i, xi, yi, zi;
// Parse arguments.
if (!PyArg_ParseTuple(args, "O!O!O!O!ddll",
&PyArray_Type, &py_pos,
&PyArray_Type, &py_vel,
&PyArray_Type, &py_force,
&PyArray_Type, &py_imass,
&delta_t, &half_delta_t,
&npart, &dim)){
return NULL;
}
// Get underlying arrays from numpy arrays.
npy_float64 *pos = (npy_float64*)PyArray_DATA(py_pos);
npy_float64 *vel = (npy_float64*)PyArray_DATA(py_vel);
npy_float64 *force = (npy_float64*)PyArray_DATA(py_force);
npy_float64 *imass = (npy_float64*)PyArray_DATA(py_imass);
// Update positions and velocity
for(i = 0; i < npart; i++){
xi = 3*i;
yi = 3*i + 1;
zi = 3*i + 2;
vel[xi] += half_delta_t * force[xi] * imass[i];
vel[yi] += half_delta_t * force[yi] * imass[i];
vel[zi] += half_delta_t * force[zi] * imass[i];
pos[xi] += delta_t * vel[xi];
pos[yi] += delta_t * vel[yi];
pos[zi] += delta_t * vel[zi];
}
Py_RETURN_NONE;
}
static PyObject *step2(PyObject *self, PyObject *args) {
// Input variables:
npy_int64 npart, dim;
npy_float64 half_delta_t;
PyArrayObject *py_vel, *py_force, *py_imass;
// Internal variables:
npy_int64 i, xi, yi, zi;
// Parse arguments.
if (!PyArg_ParseTuple(args, "O!O!O!dll",
&PyArray_Type, &py_vel,
&PyArray_Type, &py_force,
&PyArray_Type, &py_imass,
&half_delta_t,
&npart, &dim)){
return NULL;
}
// Get underlying arrays from numpy arrays.
npy_float64 *vel = (npy_float64*)PyArray_DATA(py_vel);
npy_float64 *force = (npy_float64*)PyArray_DATA(py_force);
npy_float64 *imass = (npy_float64*)PyArray_DATA(py_imass);
// Update positions and velocity
for(i = 0; i < npart; i++){
xi = 3*i;
yi = 3*i + 1;
zi = 3*i + 2;
vel[xi] += half_delta_t * force[xi] * imass[i];
vel[yi] += half_delta_t * force[yi] * imass[i];
vel[zi] += half_delta_t * force[zi] * imass[i];
}
Py_RETURN_NONE;
}
As can be seen in the C-code, there is some boilerplate code and we make use of PyArg_ParseTuple in order to parse the parameters to the function.
Step 2. Creating a setup.py file and compiling¶
The C-code can be compiled using a setup.py file.
Show/hide the contents of the setup.py file »
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
"""A script for building the C Velocity Verlet extension."""
from setuptools import (
setup,
Extension,
)
import numpy as np
CMODULE = Extension(
'vvintegrator',
sources=['vvintegrator.c'],
extra_compile_args=['-Ofast', '-march=native']
)
setup(
name='PyRETIS Velocity Verlet C extension',
description='C extension for the Velocity Verlet integrator.',
ext_modules=[CMODULE],
include_dirs=[np.get_include()],
)
The setup.py file is used to compile via the command
python setup.py build_ext --inplace
Here, build_ext is used to tell setup.py to compile the C extension and
the --inplace will put the compiled extensions into the directory you
have the source code in.
Step 3. Creating a new Python class for the engine¶
The final step is to create a Python class which is making use of the C-code.
Show/hide the contents of the new Python class »
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
"""Example of using a integration routine implemented in C."""
import logging
import os
import sys
from pyretis.engines import MDEngine
logger = logging.getLogger(__name__) # pylint: disable=invalid-name
logger.addHandler(logging.NullHandler())
sys.path.insert(0, os.path.abspath(os.path.dirname(__file__)))
try:
import vvintegrator
except ImportError:
MSG = ('Could not import external C library.'
'\nPlease compile with: "python setup.py build_ext --inplace"')
logger.critical(MSG)
raise ImportError(MSG)
__all__ = ['VelocityVerletC']
class VelocityVerletC(MDEngine):
"""VelocityVerletC(MDEngine).
This class defines the Velocity Verlet integrator.
Attributes
----------
timestep : float
The time step.
half_timestep : float
The half of the time step.
desc : string
Description of the integrator.
"""
def __init__(self, timestep,
desc='The velocity verlet integrator (C)'):
"""Set up the Velocity Verlet integrator.
Parameters
----------
timestep : float
The time step.
desc : string
Description of the integrator.
"""
super().__init__(timestep, desc, dynamics='NVE')
self.half_timestep = self.timestep * 0.5
def integration_step(self, system):
"""Velocity Verlet integration, one time step.
Parameters
----------
system : object like :py:class:`.System`
The system to integrate/act on. Assumed to have a particle
list in `system.particles`.
Returns
-------
out : None
Does not return anything, but alters the state of the given
`system`.
"""
particles = system.particles
vvintegrator.step1(
particles.pos,
particles.vel,
particles.force,
particles.imass,
self.timestep,
self.half_timestep,
particles.npart,
particles.dim
)
system.potential_and_force()
vvintegrator.step2(
particles.vel,
particles.force,
particles.imass,
self.half_timestep,
particles.npart,
particles.dim
)
You can now use the new integrator, for instance by adding the following engine section to the input file:
Engine
------
class = VelocityVerletC
timestep = 0.002
module = vvintegratorc.py
Comparison of the FORTRAN and C code¶
As you may have noticed, the FORTRAN code we have added is somewhat more to the point compared to the C-code we wrote. The C-code could, for instance, be simplified by making use of Cython, and you are encouraged to try this out.
The two Python classes we created are very similar. This means
that it is relatively little work to switch between the two
libraries from Python’s point of view. This is also evident in the
diff of the two modules shown below.
Show/hide the diff of the two Python classes »
--- /builds/pyretis/pyretis/docs/_static/examples/extending-example/engine/vvintegratorf.py
+++ /builds/pyretis/pyretis/docs/_static/examples/extending-example/engine/vvintegratorc.py
@@ -1,7 +1,7 @@
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
-"""Example of using a integration routine implemented in FORTRAN."""
+"""Example of using a integration routine implemented in C."""
import logging
import os
import sys
@@ -10,19 +10,19 @@
logger.addHandler(logging.NullHandler())
sys.path.insert(0, os.path.abspath(os.path.dirname(__file__)))
try:
- from vvintegrator import vvintegrator
+ import vvintegrator
except ImportError:
- MSG = ('Could not import external FORTRAN library.'
- '\nPlease compile with "make"!')
+ MSG = ('Could not import external C library.'
+ '\nPlease compile with: "python setup.py build_ext --inplace"')
logger.critical(MSG)
raise ImportError(MSG)
-__all__ = ['VelocityVerletF']
+__all__ = ['VelocityVerletC']
-class VelocityVerletF(MDEngine):
- """VelocityVerletF(MDEngine).
+class VelocityVerletC(MDEngine):
+ """VelocityVerletC(MDEngine).
This class defines the Velocity Verlet integrator.
@@ -31,14 +31,14 @@
timestep : float
The time step.
half_timestep : float
- The half of the timestep.
+ The half of the time step.
desc : string
Description of the integrator.
"""
def __init__(self, timestep,
- desc='The velocity verlet integrator (FORTRAN)'):
+ desc='The velocity verlet integrator (C)'):
"""Set up the Velocity Verlet integrator.
Parameters
@@ -69,18 +69,22 @@
"""
particles = system.particles
- particles.pos, particles.vel = vvintegrator.step1(
+ vvintegrator.step1(
particles.pos,
particles.vel,
particles.force,
particles.imass,
self.timestep,
- self.half_timestep
+ self.half_timestep,
+ particles.npart,
+ particles.dim
)
system.potential_and_force()
- particles.vel = vvintegrator.step2(
+ vvintegrator.step2(
particles.vel,
particles.force,
particles.imass,
- self.half_timestep
+ self.half_timestep,
+ particles.npart,
+ particles.dim
)
Creating a force field with C or FORTRAN¶
Evaluation of the forces will typically be the most time-consuming part of your simulation. If you are running PyRETIS with internal engines, there can be a lot to gain by implementing the force evaluation in C or FORTRAN. In this section, we will give a short example of how this can be done. The approach is similar to the approach for the engine, and we will do the following:
- We write the code responsible for the actual evaluation of forces in an external library.
- We compile the code. Here we do one of the following:
- For C, we create a
setup.pywhich is used to compile. - For FORTRAN, make use of a
Makefileand the program f2py.
- For C, we create a
- We write a python module containing a new
PotentialFunctionsub-class representing the new engine. This class makes use of the code which we created in steps 1 and 2.
As you may have noticed, in step 3 above, we said that we will sub-class
PotentialFunction. This is because a force field is made up
of several potential functions, and the actual computations are carried out
by the potential functions, and not the force field. So effectively, we will
be creating new potential functions to use in a force field.
To be concrete, we will implement the Lennard-Jones potential function.
Writing a new potential with FORTRAN¶
We will now create a new potential function by writing the external library in FORTRAN. This is done in the following steps:
Step 1. Creating the FORTRAN code¶
For the new potential function, we add methods for calculating
the potential and the force. In addition, we calculate the virial.
Note: Here we also add a method to apply the periodic boundaries. Ideally, we
should use the Box object, but in order to not complicate the
FORTRAN code, by calling methods from the Python class, we simply make a new
FORTRAN method to do this.
Show/hide the FORTRAN-code for the potential »
! Copyright (c) 2023, PyRETIS Development Team.
! Distributed under the LGPLv2.1+ License. See LICENSE for more info.
module ljfortranp
implicit none
private
public :: potential, force, potential_and_force
public :: pbc_dist
contains
function pbc_dist(v, box, ibox) result(dist)
! Function to apply periodic boundaries to a given displacement.
!
! Parameters
! ----------
! v : the displacement to pbc-wrap
! box : the box lengths
! ibox : the inverse box lengths, ibox = 1.0 / box
!
! Returns
! -------
! dist : the pbc-wrapped displacement
implicit none
double precision :: dist
double precision, intent(in) :: v, box, ibox
dist = v - nint(v * ibox) * box
end function pbc_dist
subroutine potential(pos, box, ibox, lj3, lj4, offset, rcut2, ptype, n, d, p, vpot)
! Function to evaluate the Lennard-Jones potential
!
! Parameters
! ----------
! pos : positions of the particles
! box : the box lengths
! ibox : the inverse box lengths, ibox = 1.0 / box
! lj3 : Lennard-Jones parameters, 4.0 * epsilonij * sigmaij**12
! lj4 : Lennard-Jones parameters, 4.0 * epsilonij * sigmaij**6
! rcut2 : Squared cut-offs
! offset : Potential energy shift
! ptype : identifier for the particle types
! n : number of particles
! d : dimensionality of the vectors
! p : number of particle types
!
! Returns
! -------
! vpot : the potential energy
implicit none
integer, intent(in) :: n, d, p
double precision, dimension(n, d), target, intent(in) :: pos
double precision, dimension(d), intent(in) :: box, ibox
double precision, dimension(p, p), intent(in) :: lj3, lj4, offset, rcut2
integer, dimension(n), intent(in) :: ptype
double precision, intent(out) :: vpot
double precision :: rsq, r2inv, r6inv, dx, dy, dz
double precision, dimension(:), pointer :: x, y, z
integer :: i, j, itype, jtype
vpot = 0.0D0
x => pos(1:n,1)
y => pos(1:n,2)
z => pos(1:n,3)
do i=1,n-1
itype = ptype(i) + 1
do j=i+1,n
jtype = ptype(j) + 1
dx = x(i) - x(j)
dy = y(i) - y(j)
dz = z(i) - z(j)
dx = pbc_dist(dx, box(1), ibox(1))
dy = pbc_dist(dy, box(2), ibox(2))
dz = pbc_dist(dz, box(3), ibox(3))
rsq = dx*dx + dy*dy + dz*dz
if (rsq < rcut2(jtype, itype)) then
r2inv = 1.0D0 / rsq
r6inv = r2inv**3
vpot = vpot + r6inv * (lj3(jtype, itype) * r6inv - lj4(jtype, itype))
vpot = vpot - offset(jtype, itype)
end if
end do
end do
end subroutine potential
subroutine force(pos, box, ibox, lj1, lj2, rcut2, ptype, n, d, p, forces, virial)
! Function to evaluate the Lennard-Jones force
!
! Parameters
! ----------
! pos : positions of the particles
! box : the box lengths
! ibox : the inverse box lengths, ibox = 1.0 / box
! lj1 : Lennard-Jones parameters, 48.0 * epsilonij * sigmaij**12
! lj2 : Lennard-Jones parameters, 24.0 * epsilonij * sigmaij**6
! rcut2 : Squared cut-offs
! ptype : identifier for the particle types
! n : number of particles
! d : dimensionality of the vectors
! p : number of particle types
!
! Returns
! -------
! forces : the Lennard-Jones forces on the particles
! virial : the virial matrix
implicit none
integer, intent(in) :: n, d, p
double precision, dimension(n, d), target, intent(out) :: forces
double precision, dimension(d, d), intent(out) :: virial
double precision, dimension(n, d), target, intent(in) :: pos
double precision, dimension(d), intent(in) :: box, ibox
double precision, dimension(p, p), intent(in) :: lj1, lj2, rcut2
integer, dimension(n), intent(in) :: ptype
double precision, dimension(:), pointer :: x, y, z, fx, fy, fz
double precision :: rsq, r2inv, r6inv, forcelj, dx, dy, dz
double precision :: forceij_x, forceij_y, forceij_z
integer :: i, j, itype, jtype
x => pos(1:n, 1)
y => pos(1:n,2)
z => pos(1:n,3)
fx => forces(1:n,1)
fy => forces(1:n,2)
fz => forces(1:n,3)
forces = 0.0D0
virial = 0.0D0
do i=1,n-1
itype = ptype(i) + 1
do j=i+1,n
jtype = ptype(j) + 1
dx = x(i) - x(j)
dy = y(i) - y(j)
dz = z(i) - z(j)
dx = pbc_dist(dx, box(1), ibox(1))
dy = pbc_dist(dy, box(2), ibox(2))
dz = pbc_dist(dz, box(3), ibox(3))
rsq = dx*dx + dy*dy + dz*dz
if (rsq < rcut2(jtype, itype)) then
r2inv = 1.0D0 / rsq
r6inv = r2inv*r2inv*r2inv
forcelj = r2inv * r6inv * (lj1(jtype, itype) * r6inv - lj2(jtype, itype))
forceij_x = forcelj * dx
forceij_y = forcelj * dy
forceij_z = forcelj * dz
fx(i) = fx(i) + forceij_x
fy(i) = fy(i) + forceij_y
fz(i) = fz(i) + forceij_z
fx(j) = fx(j) - forceij_x
fy(j) = fy(j) - forceij_y
fz(j) = fz(j) - forceij_z
! accumulate for the virial:
virial(1,1) = virial(1,1) + forceij_x * dx
virial(1,2) = virial(1,2) + forceij_x * dy
virial(1,3) = virial(1,3) + forceij_x * dz
virial(2,1) = virial(2,1) + forceij_y * dx
virial(2,2) = virial(2,2) + forceij_y * dy
virial(2,3) = virial(2,3) + forceij_y * dz
virial(3,1) = virial(3,1) + forceij_z * dx
virial(3,2) = virial(3,2) + forceij_z * dy
virial(3,3) = virial(3,3) + forceij_z * dz
end if
end do
end do
end subroutine force
subroutine potential_and_force(pos, box, ibox, lj1, lj2, lj3, lj4, offset, rcut2, ptype, n, d, p, forces, virial, vpot)
! Function to evaluate the Lennard-Jones force and potential
!
! Parameters
! ----------
! pos : positions of the particles
! box : the box lengths
! ibox : the inverse box lengths, ibox = 1.0 / box
! lj1 : Lennard-Jones parameters, 48.0 * epsilonij * sigmaij**12
! lj2 : Lennard-Jones parameters, 24.0 * epsilonij * sigmaij**6
! lj3 : Lennard-Jones parameters, 4.0 * epsilonij * sigmaij**12
! lj4 : Lennard-Jones parameters, 4.0 * epsilonij * sigmaij**6
! rcut2 : Squared cut-offs
! offset : Potential energy shift
! ptype : identifier for the particle types
! n : number of particles
! d : dimensionality of the vectors
! p : number of particle types
!
! Returns
! -------
! vpot : the potential energy
! forces : the Lennard-Jones forces on the particles
! virial : the virial matrix
implicit none
integer, intent(in) :: n, d, p
double precision, dimension(n, d), target, intent(out) :: forces
double precision, dimension(d, d), intent(out) :: virial
double precision, intent(out) :: vpot
double precision, dimension(n, d), target, intent(in) :: pos
double precision, dimension(d), intent(in) :: ibox, box
double precision, dimension(p, p), intent(in) :: lj1, lj2, lj3, lj4, offset, rcut2
double precision, dimension(:), pointer :: x, y, z, fx, fy, fz
integer, dimension(n), intent(in) :: ptype
double precision :: rsq, r2inv, r6inv, forcelj, dx, dy, dz
double precision :: forceij_x, forceij_y, forceij_z
integer :: i, j, itype, jtype
forces = 0.0D0
virial = 0.0D0
vpot = 0.0D0
x => pos(1:n,1)
y => pos(1:n,2)
z => pos(1:n,3)
fx => forces(1:n,1)
fy => forces(1:n,2)
fz => forces(1:n,3)
do i=1,n-1
itype = ptype(i) + 1
do j=i+1,n
jtype = ptype(j) + 1
dx = x(i) - x(j)
dy = y(i) - y(j)
dz = z(i) - z(j)
dx = pbc_dist(dx, box(1), ibox(1))
dy = pbc_dist(dy, box(2), ibox(2))
dz = pbc_dist(dz, box(3), ibox(3))
rsq = dx*dx + dy*dy + dz*dz
if (rsq < rcut2(jtype, itype)) then
r2inv = 1.0D0 / rsq
r6inv = r2inv*r2inv*r2inv
forcelj = r2inv * r6inv * (lj1(jtype, itype) * r6inv - lj2(jtype, itype))
forceij_x = forcelj * dx
forceij_y = forcelj * dy
forceij_z = forcelj * dz
fx(i) = fx(i) + forceij_x
fy(i) = fy(i) + forceij_y
fz(i) = fz(i) + forceij_z
fx(j) = fx(j) - forceij_x
fy(j) = fy(j) - forceij_y
fz(j) = fz(j) - forceij_z
vpot = vpot + r6inv * (lj3(jtype, itype) * r6inv - lj4(jtype, itype))
vpot = vpot - offset(jtype, itype)
! accumulate for the virial:
virial(1,1) = virial(1,1) + forceij_x * dx
virial(1,2) = virial(1,2) + forceij_x * dy
virial(1,3) = virial(1,3) + forceij_x * dz
virial(2,1) = virial(2,1) + forceij_y * dx
virial(2,2) = virial(2,2) + forceij_y * dy
virial(2,3) = virial(2,3) + forceij_y * dz
virial(3,1) = virial(3,1) + forceij_z * dx
virial(3,2) = virial(3,2) + forceij_z * dy
virial(3,3) = virial(3,3) + forceij_z * dz
end if
end do
end do
end subroutine potential_and_force
end module ljfortranp
Step 2. Creating the Makefile and compiling¶
The step is almost identical to the
compilation for the external engine.
The Makefile is given below, and note here that we are assuming that the FORTRAN code
is stored in a module named ljfortranp.f90.
Show/hide the contents of the Makefile »
F2PY = f2py
F2PY_FLAGS = --fcompiler=gfortran
MODULE=ljfortranp
all: ${MODULE}.so
${MODULE}.so: ${MODULE}.f90
${F2PY} ${F2PY_FLAGS} -c $< -m ${MODULE}
clean:
find -name \*.so -delete
find -name \*.pyc -delete
find -name __pycache__ -delete
Step 3. Creating a new Python class for the potential¶
For the Python class representing the potential, we just import the module we compiled in the previous step.
Show/hide the contents of the new Python class »
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
"""Example of using a Lennard-Jones potential implemented in FORTRAN."""
import logging
import os
import sys
import numpy as np
from pyretis.forcefield.potentials import PairLennardJonesCut
from pyretis.forcefield.potentials.pairpotentials import (
generate_pair_interactions
)
logger = logging.getLogger(__name__) # pylint: disable=invalid-name
logger.addHandler(logging.NullHandler())
sys.path.insert(0, os.path.abspath(os.path.dirname(__file__)))
try:
from ljfortranp import ljfortranp
except ImportError as exc:
MSG = ('Could not import external FORTRAN library.'
'\nPlease compile with "make"!')
raise ImportError(MSG) from exc
__all__ = ['PairLennardJonesCutFp']
class PairLennardJonesCutFp(PairLennardJonesCut):
r"""class PairLennardJonesCutFp(PairLennardJonesCut).
This class implements as simple Lennard-Jones 6-12 potential which
employs a simple cut-off and can be shifted. The potential energy
(:math:`V_\text{pot}`) is defined in the usual way for an
interacting pair of particles a distance :math:`r` apart,
.. math::
V_\text{pot} = 4 \varepsilon \left( x^{12} - x^{6} \right),
where :math:`x = \sigma/r` and :math:`\varepsilon`
and :math:`\sigma` are the potential parameters. The parameters are
stored as attributes of the potential and we store one set for each
kind of pair interaction. Parameters can be generated with a
specific mixing rule by the force field.
Attributes
----------
params : dict
The parameters for the potential. This dict is assumed to
contain parameters for pairs, i.e. for interactions.
_lj : dict of numpy.array
[1] Lennard-Jones parameters used for calculation of the force.
Keys are the pairs (particle types) that may interact.
Calculated as: ``48.0 * epsilon * sigma**12``
[2] Lennard-Jones parameters used for calculation of the force.
Keys are the pairs (particle types) that may interact.
Calculated as: ``24.0 * epsilon * sigma**6``
[3] Lennard-Jones parameters used for calculation of the potential.
Keys are the pairs (particle types) that may interact.
Calculated as: ``4.0 * epsilon * sigma**12``
[4] Lennard-Jones parameters used for calculation of the potential.
Keys are the pairs (particle types) that may interact.
Calculated as: ``4.0 * epsilon * sigma**6``
_offset : numpy.array
Potential values for shifting the potential if requested.
This is the potential evaluated at the cutoff.
_rcut2 : numpy.array
The squared cut-off for each interaction type.
Keys are the pairs (particle types) that may interact.
"""
def __init__(self, dim=3, shift=True, mixing='geometric',
desc='Lennard-Jones pair potential (fortran)'):
"""Set up the Lennard-Jones potential.
Parameters
----------
dim : int
The dimensionality to use.
shift : boolean
Determines if the potential should be shifted or not.
mixing : string
Determines how we should mix potential parameters.
"""
super().__init__(dim=dim, desc=desc, mixing=mixing)
self.shift = shift
self.ntype = 0
def set_parameters(self, parameters):
"""Update all parameters.
Here, we generate pair interactions, since that is what this
potential actually is using.
Parameters
----------
parameters : dict
The input base parameters.
"""
self.params = {}
pair_param = generate_pair_interactions(parameters, self.mixing)
self.ntype = max(int(np.sqrt(len(pair_param))), 2)
self._lj = {'1': np.zeros((self.ntype, self.ntype)),
'2': np.zeros((self.ntype, self.ntype)),
'3': np.zeros((self.ntype, self.ntype)),
'4': np.zeros((self.ntype, self.ntype))}
self._rcut2 = np.zeros_like(self._lj[1])
self._offset = np.zeros_like(self._lj[1])
for pair, value in pair_param.items():
eps_ij = value['epsilon']
sig_ij = value['sigma']
rcut = value['rcut']
self._lj[1][pair] = 48.0 * eps_ij * sig_ij**12
self._lj[2][pair] = 24.0 * eps_ij * sig_ij**6
self._lj[3][pair] = 4.0 * eps_ij * sig_ij**12
self._lj[4][pair] = 4.0 * eps_ij * sig_ij**6
self._rcut2[pair] = rcut**2
vcut = 0.0
if self.shift and not np.isclose(rcut, 0):
vcut = 4.0 * eps_ij * ((sig_ij / rcut)**12 -
(sig_ij / rcut)**6)
self._offset[pair] = vcut
self.params[pair] = pair_param[pair]
def potential(self, system):
"""Calculate the potential energy for the Lennard-Jones interaction.
Parameters
----------
system : object like `System` from `pyretis.core.system`
The system we are evaluating the potential in.
Returns
-------
v_pot : float
The potential energy.
"""
particles = system.particles
box = system.box
v_pot = ljfortranp.potential(
particles.pos,
box.length,
box.ilength,
self._lj,
self._offset,
self._rcut2,
particles.ptype,
particles.npart,
box.dim,
self.ntype
)
return v_pot
def force(self, system):
"""Calculate the force for the Lennard-Jones interaction.
We also calculate the virial here, since the force
is evaluated.
Parameters
----------
system : object like `System` from `pyretis.core.system`
The system we are evaluating the force in.
Returns
-------
forces : numpy.array
The forces on the particles.
virial : numpy.array
The virial obtained from the forces.
"""
particles = system.particles
box = system.box
forces, virial = ljfortranp.force(
particles.pos,
box.length,
box.ilength,
self._lj,
self._rcut2,
particles.ptype,
particles.npart,
box.dim,
self.ntype
)
return forces, virial
def potential_and_force(self, system):
"""Calculate potential and force for the Lennard-Jones interaction.
Since the force is evaluated, the virial is also calculated.
Parameters
----------
system : object like `System` from `pyretis.core.system`
The system we are evaluating the potential and force in.
Note
----
Currently, the virial is only calculated for all the particles.
It is not calculated as a virial per atom. The virial
per atom might be useful to obtain a local pressure or stress,
however, this needs some consideration. Perhaps it's best to
fully implement this as a method of planes or something similar.
Returns
-------
out[0] : float
The potential energy as a float.
out[1] : numpy.array
The force as a numpy.array of the same shape as the
positions in `particles.pos`.
out[2] : numpy.array
The virial, as a symmetric matrix with dimensions
(dim, dim) where dim is given by the box/system dimensions.
"""
particles = system.particles
box = system.box
forces, virial, vpot = ljfortranp.potential_and_force(
particles.pos,
box.length,
box.ilength,
self._lj,
self._offset,
self._rcut2,
particles.ptype,
particles.npart,
box.dim,
self.ntype
)
return vpot, forces, virial
You can now use the new potential, for instance by adding the following forcefield and potential sections to the input file:
Forcefield
----------
description = Lennard-Jones evaluated in FORTRAN
Potential
---------
class = PairLennardJonesCutFp
module = ljpotentialfp.py
shift = True
dim = 3
mixing = geometric
parameter 0 = {'sigma': 1, 'epsilon': 1, 'factor': 2.5}
Writing a new potential with C¶
We will now create a new potential function by writing the external library in C. This is done in the following steps:
Step 1. Creating the C-code¶
We set up the C-code as in the engine example.
Show/hide the C-code for the potential »
/* Copyright (c) 2023, PyRETIS Development Team.
Distributed under the LGPLv2.1+ License. See LICENSE for more info. */
#define NPY_NO_DEPRECATED_API NPY_1_7_API_VERSION
#include <Python.h>
#include <numpy/arrayobject.h>
#include <math.h>
// Forward function declaration.
static PyObject *potential(PyObject *self, PyObject *args);
static PyObject *force(PyObject *self, PyObject *args);
static PyObject *force_and_pot(PyObject *self, PyObject *args);
// Boilerplate: function list.
static PyMethodDef ljmethods[] = {
{ "potential", potential, METH_VARARGS, "Calculate potential energy."},
{ "force", force, METH_VARARGS, "Calculate force."},
{ "force_and_pot", force_and_pot, METH_VARARGS, "Calculate force and potential energy."},
{ NULL, NULL, 0, NULL } /* Sentinel */
};
static struct PyModuleDef ljc =
{
PyModuleDef_HEAD_INIT,
"ljc",
"Compute Lennard-Jones interactions",
-1,
ljmethods
};
// Boilerplate: Module initialization.
PyMODINIT_FUNC PyInit_ljc(void) {
import_array();
return PyModule_Create(&ljc);
}
static inline npy_float64 pbc_dist(npy_float64 x,
npy_float64 box,
npy_float64 ibox) {
return x - nearbyint(x * ibox) * box;
}
static PyObject *potential(PyObject *self, PyObject *args) {
// Input variables:
npy_int64 npart, dim, ntype;
npy_int64 itype, loc;
PyArrayObject *py_pos, *py_box, *py_ibox, *py_lj3, *py_lj4, *py_rcut2, *py_offset, *py_ptype;
// Internal variables:
npy_float64 dx, dy, dz, rsq, r2inv, r6inv;
npy_int64 i, xi, yi, zi;
npy_int64 j, xj, yj, zj;
// Parse arguments.
if (!PyArg_ParseTuple(args, "O!O!O!O!O!O!O!O!lll",
&PyArray_Type, &py_pos,
&PyArray_Type, &py_box,
&PyArray_Type, &py_ibox,
&PyArray_Type, &py_lj3,
&PyArray_Type, &py_lj4,
&PyArray_Type, &py_offset,
&PyArray_Type, &py_rcut2,
&PyArray_Type, &py_ptype,
&npart, &dim, &ntype)){
return NULL;
}
// Get underlying arrays from numpy arrays.
npy_float64 *pos = (npy_float64*)PyArray_DATA(py_pos);
npy_float64 *box = (npy_float64*)PyArray_DATA(py_box);
npy_float64 *ibox = (npy_float64*)PyArray_DATA(py_ibox);
npy_float64 *lj3 = (npy_float64*)PyArray_DATA(py_lj3);
npy_float64 *lj4 = (npy_float64*)PyArray_DATA(py_lj4);
npy_float64 *rcut2 = (npy_float64*)PyArray_DATA(py_rcut2);
npy_float64 *offset = (npy_float64*)PyArray_DATA(py_offset);
npy_int64 *ptype = (npy_int64*)PyArray_DATA(py_ptype);
npy_float64 vpot = 0.0;
// Calculate potential:
for(i = 0; i < npart-1; i++){
xi = 3*i;
yi = 3*i + 1;
zi = 3*i + 2;
itype = ptype[i];
for (j = i + 1; j < npart; j++){
loc = itype + ntype * ptype[j];
xj = 3*j;
yj = 3*j + 1;
zj = 3*j + 2;
dx = pos[xi] - pos[xj];
dy = pos[yi] - pos[yj];
dz = pos[zi] - pos[zj];
dx = pbc_dist(dx, box[0], ibox[0]);
dy = pbc_dist(dy, box[1], ibox[1]);
dz = pbc_dist(dz, box[2], ibox[2]);
rsq = dx*dx + dy*dy + dz*dz;
if (rsq < rcut2[loc]){
r2inv = 1.0 / rsq;
r6inv = r2inv*r2inv*r2inv;
vpot += r6inv * (lj3[loc] * r6inv - lj4[loc]) - offset[loc];
}
}
}
/* Clean up */
/* Build the output tuple */
PyObject *ret = Py_BuildValue("d", vpot);
return ret;
}
static PyObject *force(PyObject *self, PyObject *args) {
// Input variables:
npy_int64 npart, dim, ntype;
npy_int64 itype, loc;
PyArrayObject *py_pos, *py_box, *py_ibox, *py_force, *py_virial;
PyArrayObject *py_lj1, *py_lj2, *py_rcut2, *py_ptype;
// Internal variables:
npy_float64 dx, dy, dz, rsq, r2inv, r6inv;
npy_float64 forcelj, fx, fy, fz;
npy_int64 i, xi, yi, zi;
npy_int64 j, xj, yj, zj;
// Parse arguments.
if (!PyArg_ParseTuple(args, "O!O!O!O!O!O!O!O!O!lll",
&PyArray_Type, &py_pos,
&PyArray_Type, &py_box,
&PyArray_Type, &py_ibox,
&PyArray_Type, &py_lj1,
&PyArray_Type, &py_lj2,
&PyArray_Type, &py_rcut2,
&PyArray_Type, &py_ptype,
&PyArray_Type, &py_force,
&PyArray_Type, &py_virial,
&npart, &dim, &ntype)){
return NULL;
}
// Get underlying arrays from numpy arrays.
npy_float64 *force = (npy_float64*)PyArray_DATA(py_force);
npy_float64 *virial = (npy_float64*)PyArray_DATA(py_virial);
npy_float64 *pos = (npy_float64*)PyArray_DATA(py_pos);
npy_float64 *box = (npy_float64*)PyArray_DATA(py_box);
npy_float64 *ibox = (npy_float64*)PyArray_DATA(py_ibox);
npy_float64 *lj1 = (npy_float64*)PyArray_DATA(py_lj1);
npy_float64 *lj2 = (npy_float64*)PyArray_DATA(py_lj2);
npy_float64 *rcut2 = (npy_float64*)PyArray_DATA(py_rcut2);
npy_int64 *ptype = (npy_int64*)PyArray_DATA(py_ptype);
// Create array for forces:
//PyObject *ret = PyArray_SimpleNew(dim, test, NPY_DOUBLE);
// Zero virial:
for(i = 0; i < dim*dim; i++) {
virial[i] = 0;
}
// Set all forces to zero.
for(i = 0; i < npart; i++) {
force[3*i] = 0;
force[3*i+1] = 0;
force[3*i+2] = 0;
}
// Calculate forces:
for(i = 0; i < npart-1; i++){
xi = 3*i;
yi = 3*i + 1;
zi = 3*i + 2;
itype = ptype[i];
for (j = i + 1; j < npart; j++){
loc = itype + ntype * ptype[j];
xj = 3*j;
yj = 3*j + 1;
zj = 3*j + 2;
dx = pos[xi] - pos[xj];
dy = pos[yi] - pos[yj];
dz = pos[zi] - pos[zj];
dx = pbc_dist(dx, box[0], ibox[0]);
dy = pbc_dist(dy, box[1], ibox[1]);
dz = pbc_dist(dz, box[2], ibox[2]);
rsq = dx*dx + dy*dy + dz*dz;
if (rsq < rcut2[loc]){
r2inv = 1.0 / rsq;
r6inv = r2inv*r2inv*r2inv;
forcelj = r2inv * r6inv * (lj1[loc] * r6inv - lj2[loc]);
fx = forcelj * dx;
fy = forcelj * dy;
fz = forcelj * dz;
force[xi] += fx;
force[yi] += fy;
force[zi] += fz;
force[xj] -= fx;
force[yj] -= fy;
force[zj] -= fz;
virial[0] += fx*dx;
virial[1] += fx*dy;
virial[2] += fx*dz;
virial[3] += fy*dx;
virial[4] += fy*dy;
virial[5] += fy*dz;
virial[6] += fz*dx;
virial[7] += fz*dy;
virial[8] += fz*dz;
}
}
}
Py_RETURN_NONE;
}
static PyObject *force_and_pot(PyObject *self, PyObject *args) {
// Input variables:
npy_int64 npart, dim, ntype;
npy_int64 itype, loc;
PyArrayObject *py_pos, *py_box, *py_ibox, *py_force, *py_virial;
PyArrayObject *py_lj1, *py_lj2, *py_lj3, *py_lj4, *py_rcut2, *py_offset, *py_ptype;
// Internal variables:
npy_float64 dx, dy, dz, rsq, r2inv, r6inv;
npy_float64 forcelj, fx, fy, fz;
npy_int64 i, xi, yi, zi;
npy_int64 j, xj, yj, zj;
// Parse arguments.
if (!PyArg_ParseTuple(args, "O!O!O!O!O!O!O!O!O!O!O!O!lll",
&PyArray_Type, &py_pos,
&PyArray_Type, &py_box,
&PyArray_Type, &py_ibox,
&PyArray_Type, &py_lj1,
&PyArray_Type, &py_lj2,
&PyArray_Type, &py_lj3,
&PyArray_Type, &py_lj4,
&PyArray_Type, &py_offset,
&PyArray_Type, &py_rcut2,
&PyArray_Type, &py_ptype,
&PyArray_Type, &py_force,
&PyArray_Type, &py_virial,
&npart, &dim, &ntype)){
return NULL;
}
// Get underlying arrays from numpy arrays.
npy_float64 *force = (npy_float64*)PyArray_DATA(py_force);
npy_float64 *virial = (npy_float64*)PyArray_DATA(py_virial);
npy_float64 *pos = (npy_float64*)PyArray_DATA(py_pos);
npy_float64 *box = (npy_float64*)PyArray_DATA(py_box);
npy_float64 *ibox = (npy_float64*)PyArray_DATA(py_ibox);
npy_float64 *lj1 = (npy_float64*)PyArray_DATA(py_lj1);
npy_float64 *lj2 = (npy_float64*)PyArray_DATA(py_lj2);
npy_float64 *lj3 = (npy_float64*)PyArray_DATA(py_lj3);
npy_float64 *lj4 = (npy_float64*)PyArray_DATA(py_lj4);
npy_float64 *offset = (npy_float64*)PyArray_DATA(py_offset);
npy_float64 *rcut2 = (npy_float64*)PyArray_DATA(py_rcut2);
npy_int64 *ptype = (npy_int64*)PyArray_DATA(py_ptype);
npy_float64 vpot = 0.0;
// Create array for forces:
//PyObject *ret = PyArray_SimpleNew(dim, test, NPY_DOUBLE);
// Zero virial:
for(i = 0; i < dim*dim; i++) {
virial[i] = 0;
}
// Set all forces to zero.
for(i = 0; i < npart; i++) {
force[3*i] = 0;
force[3*i+1] = 0;
force[3*i+2] = 0;
}
// Calculate forces:
for(i = 0; i < npart-1; i++){
xi = 3*i;
yi = 3*i + 1;
zi = 3*i + 2;
itype = ptype[i];
for (j = i + 1; j < npart; j++){
loc = itype + ntype * ptype[j];
xj = 3*j;
yj = 3*j + 1;
zj = 3*j + 2;
dx = pos[xi] - pos[xj];
dy = pos[yi] - pos[yj];
dz = pos[zi] - pos[zj];
dx = pbc_dist(dx, box[0], ibox[0]);
dy = pbc_dist(dy, box[1], ibox[1]);
dz = pbc_dist(dz, box[2], ibox[2]);
rsq = dx*dx + dy*dy + dz*dz;
if (rsq < rcut2[loc]){
r2inv = 1.0 / rsq;
r6inv = r2inv*r2inv*r2inv;
forcelj = r2inv * r6inv * (lj1[loc] * r6inv - lj2[loc]);
vpot += r6inv * (lj3[loc] * r6inv - lj4[loc]) - offset[loc];
fx = forcelj * dx;
fy = forcelj * dy;
fz = forcelj * dz;
force[xi] += fx;
force[yi] += fy;
force[zi] += fz;
force[xj] -= fx;
force[yj] -= fy;
force[zj] -= fz;
virial[0] += fx*dx;
virial[1] += fx*dy;
virial[2] += fx*dz;
virial[3] += fy*dx;
virial[4] += fy*dy;
virial[5] += fy*dz;
virial[6] += fz*dx;
virial[7] += fz*dy;
virial[8] += fz*dz;
}
}
}
PyObject *ret = Py_BuildValue("d", vpot);
return ret;
}
Step 2. Creating a setup.py file and compiling¶
In order to compile the C-code we just created, we make use of a setup.py file
which is almost identical to the one we created for the engine.
Show/hide the contents of the setup.py file »
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
"""A script for building the C Lennard-Jones extension."""
from setuptools import (
setup,
Extension,
)
import numpy as np
LJMODULE = Extension(
'ljc',
sources=['ljc.c'],
extra_compile_args=["-Ofast", "-march=native"]
)
setup(
name="PyRETIS Lennard-Jones C extension",
description="C extension for the Lennard-Jones potential.",
ext_modules=[LJMODULE],
include_dirs=[np.get_include()],
)
As before, the setup.py file is used to compile via the command
python setup.py build_ext --inplace
Note that we assume that the C-code is stored in a file named ljc.c.
Step 3. Creating a new Python class for the potential¶
The final step is to create a Python class which is making use of the C-code.
Show/hide the contents of the new Python class »
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
"""Example of using a Lennard-Jones potential implemented in C."""
import logging
import os
import sys
import numpy as np
from pyretis.forcefield.potentials import PairLennardJonesCut
from pyretis.forcefield.potentials.pairpotentials import (
generate_pair_interactions
)
logger = logging.getLogger(__name__) # pylint: disable=invalid-name
logger.addHandler(logging.NullHandler())
sys.path.insert(0, os.path.abspath(os.path.dirname(__file__)))
try:
import ljc
except ImportError as exc:
MSG = ('Could not import external C library.'
'\nPlease compile with: "python setup.py build_ext --inplace"')
raise ImportError(MSG) from exc
__all__ = ['PairLennardJonesCutC']
class PairLennardJonesCutC(PairLennardJonesCut):
r"""class PairLennardJonesCutC(PairLennardJonesCut).
This class implements as simple Lennard-Jones 6-12 potential which
employs a simple cut-off and can be shifted. The potential energy
(:math:`V_\text{pot}`) is defined in the usual way for an
interacting pair of particles a distance :math:`r` apart,
.. math::
V_\text{pot} = 4 \varepsilon \left( x^{12} - x^{6} \right),
where :math:`x = \sigma/r` and :math:`\varepsilon`
and :math:`\sigma` are the potential parameters. The parameters are
stored as attributes of the potential and we store one set for each
kind of pair interaction. Parameters can be generated with a
specific mixing rule by the force field.
Attributes
----------
params : dict
The parameters for the potential. This dict is assumed to
contain parameters for pairs, i.e. for interactions.
_lj : dict of numpy.array
[1] Lennard-Jones parameters used for calculation of the force.
Keys are the pairs (particle types) that may interact.
Calculated as: ``48.0 * epsilon * sigma**12``
[2] Lennard-Jones parameters used for calculation of the force.
Keys are the pairs (particle types) that may interact.
Calculated as: ``24.0 * epsilon * sigma**6``
[3] Lennard-Jones parameters used for calculation of the potential.
Keys are the pairs (particle types) that may interact.
Calculated as: ``4.0 * epsilon * sigma**12``
[4] Lennard-Jones parameters used for calculation of the potential.
Keys are the pairs (particle types) that may interact.
Calculated as: ``4.0 * epsilon * sigma**6``
_offset : numpy.array
Potential values for shifting the potential if requested.
This is the potential evaluated at the cutoff.
_rcut2 : numpy.array
The squared cut-off for each interaction type.
Keys are the pairs (particle types) that may interact.
"""
def __init__(self, dim=3, shift=True, mixing='geometric',
desc='Lennard-Jones pair potential (C)'):
"""Initialise the Lennard-Jones potential.
Parameters
----------
dim : int
The dimensionality to use.
shift : boolean
Determines if the potential should be shifted or not.
mixing : string
Determines how we should mix potential parameters.
"""
super().__init__(dim=dim, desc=desc, mixing=mixing)
self.shift = shift
self.ntype = 0
def set_parameters(self, parameters):
"""Update all parameters.
Here, we generate pair interactions, since that is what this
potential actually is using.
Parameters
----------
parameters : dict
The input base parameters.
"""
self.params = {}
pair_param = generate_pair_interactions(parameters, self.mixing)
self.ntype = max(int(np.sqrt(len(pair_param))), 2)
self._lj = {'1': np.zeros((self.ntype, self.ntype)),
'2': np.zeros((self.ntype, self.ntype)),
'3': np.zeros((self.ntype, self.ntype)),
'4': np.zeros((self.ntype, self.ntype))}
self._rcut2 = np.zeros_like(self._lj[1])
self._offset = np.zeros_like(self._lj[1])
for pair, value in pair_param.items():
eps_ij = value['epsilon']
sig_ij = value['sigma']
rcut = value['rcut']
self._lj[1][pair] = 48.0 * eps_ij * sig_ij**12
self._lj[2][pair] = 24.0 * eps_ij * sig_ij**6
self._lj[3][pair] = 4.0 * eps_ij * sig_ij**12
self._lj[4][pair] = 4.0 * eps_ij * sig_ij**6
self._rcut2[pair] = rcut**2
vcut = 0.0
if self.shift and not np.isclose(rcut, 0):
vcut = 4.0 * eps_ij * ((sig_ij / rcut)**12 -
(sig_ij / rcut)**6)
self._offset[pair] = vcut
self.params[pair] = pair_param[pair]
def potential(self, system):
"""Calculate the potential energy for the Lennard-Jones interaction.
Parameters
----------
system : object like `System` from `pyretis.core.system`
The system we are evaluating the potential in.
Returns
-------
v_pot : float
The potential energy.
"""
particles = system.particles
box = system.box
v_pot = ljc.potential(
particles.pos,
box.length,
box.ilength,
self._lj,
self._offset,
self._rcut2,
particles.ptype,
particles.npart,
box.dim,
self.ntype
)
return v_pot
def force(self, system):
"""Calculate the force for the Lennard-Jones interaction.
We also calculate the virial here, since the force
is evaluated.
Parameters
----------
system : object like `System` from `pyretis.core.system`
The system we are evaluating the force in.
Returns
-------
forces : numpy.array
The forces on the particles.
virial : numpy.array
The virial obtained from the forces.
"""
particles = system.particles
box = system.box
forces = np.zeros((particles.npart, box.dim))
virial = np.zeros((box.dim, box.dim))
ljc.force(
particles.pos,
box.length,
box.ilength,
self._lj,
self._rcut2,
particles.ptype,
forces,
virial,
particles.npart,
box.dim,
self.ntype
)
return forces, virial
def potential_and_force(self, system):
"""Calculate potential and force for the Lennard-Jones interaction.
Since the force is evaluated, the virial is also calculated.
Parameters
----------
system : object like `System` from `pyretis.core.system`
The system we are evaluating the potential and force in.
Note
----
Currently, the virial is only calculated for all the particles.
It is not calculated as a virial per atom. The virial
per atom might be useful to obtain a local pressure or stress,
however, this needs some consideration. Perhaps it's best to
fully implement this as a method of planes or something similar.
Returns
-------
out[0] : float
The potential energy as a float.
out[1] : numpy.array
The force as a numpy.array of the same shape as the
positions in `particles.pos`.
out[2] : numpy.array
The virial, as a symmetric matrix with dimensions
(dim, dim) where dim is given by the box/system dimensions.
"""
particles = system.particles
box = system.box
forces = np.zeros((particles.npart, box.dim))
virial = np.zeros((box.dim, box.dim))
vpot = ljc.force_and_pot(
particles.pos,
box.length,
box.ilength,
self._lj,
self._offset,
self._rcut2,
particles.ptype,
forces,
virial,
particles.npart,
box.dim,
self.ntype
)
return vpot, forces, virial
You can now use the new potential, for instance by adding the following forcefield and potential sections to the input file:
Forcefield settings
--------------------
description = Lennard-Jones evaluated in C
Potential
---------
class = PairLennardJonesCutC
module = ljpotentialc.py
shift = True
dim = 3
mixing = geometric
parameter 0 = {'sigma': 1.0, 'epsilon': 1.0, 'rcut': 2.5}
Again, we note that the two Python classes we created (for FORTRAN and C) are very similar.
The diff of the two modules shown below.
Show/hide the diff of the two Python classes »
--- /builds/pyretis/pyretis/docs/_static/examples/extending-example/potential/ljpotentialfp.py
+++ /builds/pyretis/pyretis/docs/_static/examples/extending-example/potential/ljpotentialc.py
@@ -1,7 +1,7 @@
# -*- coding: utf-8 -*-
# Copyright (c) 2023, PyRETIS Development Team.
# Distributed under the LGPLv2.1+ License. See LICENSE for more info.
-"""Example of using a Lennard-Jones potential implemented in FORTRAN."""
+"""Example of using a Lennard-Jones potential implemented in C."""
import logging
import os
import sys
@@ -15,18 +15,18 @@
sys.path.insert(0, os.path.abspath(os.path.dirname(__file__)))
try:
- from ljfortranp import ljfortranp
+ import ljc
except ImportError as exc:
- MSG = ('Could not import external FORTRAN library.'
- '\nPlease compile with "make"!')
+ MSG = ('Could not import external C library.'
+ '\nPlease compile with: "python setup.py build_ext --inplace"')
raise ImportError(MSG) from exc
-__all__ = ['PairLennardJonesCutFp']
-
-
-class PairLennardJonesCutFp(PairLennardJonesCut):
- r"""class PairLennardJonesCutFp(PairLennardJonesCut).
+__all__ = ['PairLennardJonesCutC']
+
+
+class PairLennardJonesCutC(PairLennardJonesCut):
+ r"""class PairLennardJonesCutC(PairLennardJonesCut).
This class implements as simple Lennard-Jones 6-12 potential which
employs a simple cut-off and can be shifted. The potential energy
@@ -71,8 +71,8 @@
"""
def __init__(self, dim=3, shift=True, mixing='geometric',
- desc='Lennard-Jones pair potential (fortran)'):
- """Set up the Lennard-Jones potential.
+ desc='Lennard-Jones pair potential (C)'):
+ """Initialise the Lennard-Jones potential.
Parameters
----------
@@ -141,7 +141,7 @@
"""
particles = system.particles
box = system.box
- v_pot = ljfortranp.potential(
+ v_pot = ljc.potential(
particles.pos,
box.length,
box.ilength,
@@ -176,13 +176,17 @@
"""
particles = system.particles
box = system.box
- forces, virial = ljfortranp.force(
+ forces = np.zeros((particles.npart, box.dim))
+ virial = np.zeros((box.dim, box.dim))
+ ljc.force(
particles.pos,
box.length,
box.ilength,
self._lj,
self._rcut2,
particles.ptype,
+ forces,
+ virial,
particles.npart,
box.dim,
self.ntype
@@ -221,7 +225,9 @@
"""
particles = system.particles
box = system.box
- forces, virial, vpot = ljfortranp.potential_and_force(
+ forces = np.zeros((particles.npart, box.dim))
+ virial = np.zeros((box.dim, box.dim))
+ vpot = ljc.force_and_pot(
particles.pos,
box.length,
box.ilength,
@@ -229,6 +235,8 @@
self._offset,
self._rcut2,
particles.ptype,
+ forces,
+ virial,
particles.npart,
box.dim,
self.ntype
Comparison of the C, FORTRAN and a Numpy implementation¶
In the figure below, we show some sample timings using the modules you have just created two Python implementations (one is in pure Python, while the other is using Numpy).
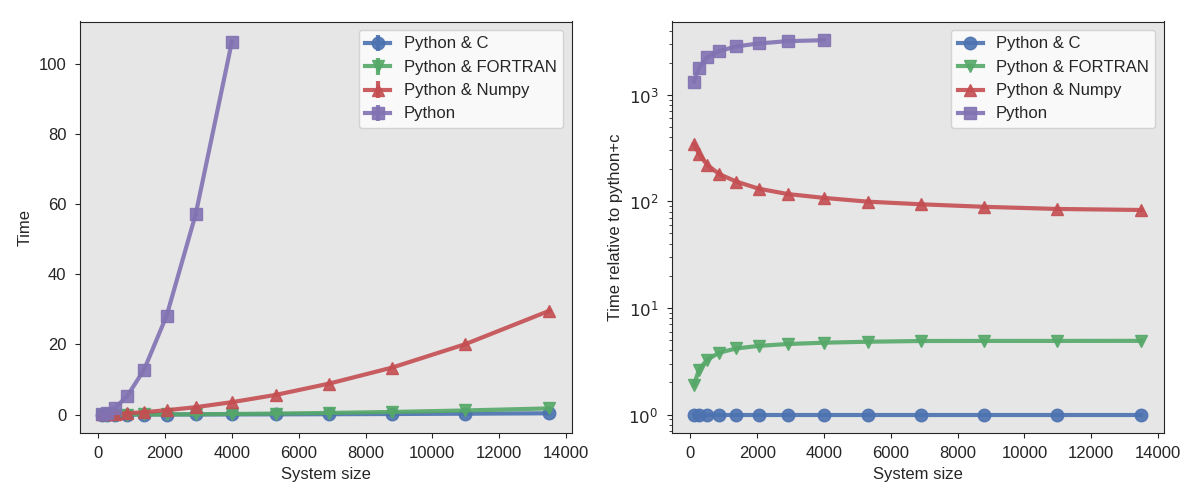
Fig. 34 Sample timing results when using the external modules written in C and FORTRAN compared with Python implementations.¶
OpenMP: Parallel evaluation of the force¶
In both the C module and the FORTRAN module, we created for evaluation of the force, it is possible to speed up the force evaluation by, for instance, making use of OpenMP directives. We just give a very brief example below, and leave the rest to you.
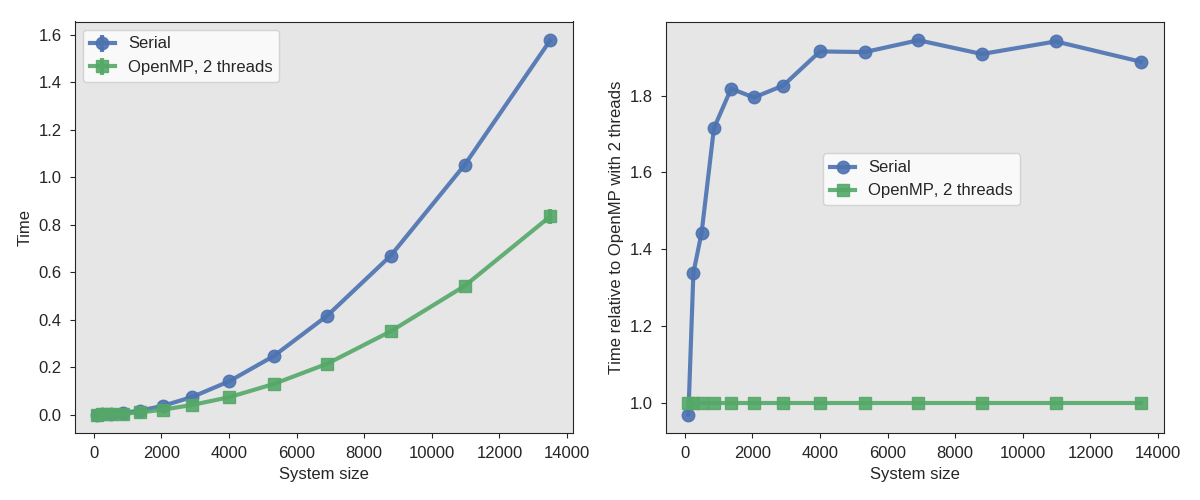
Fig. 35 Sample results using OpenMP while calculating the Lennard-Jones potential energy. The left figure shows the actual time used (average over 5 independent runs), while the right figure shows the time used relative to each other.¶
Show/hide a short OpenMP aware FORTRAN example »
subroutine potential(pos, box, ibox, lj3, lj4, offset, rcut2, ptype, n, d, p, vpot) ! Function to evaluate the Lennard-Jones potential ! ! Parameters ! ---------- ! pos : positions of the particles ! box : the box lengths ! ibox : the inverse box lengths, ibox = 1.0 / box ! lj3 : Lennard-Jones parameters, 4.0 * epsilonij * sigmaij**12 ! lj4 : Lennard-Jones parameters, 4.0 * epsilonij * sigmaij**6 ! rcut2 : Squared cut-offs ! offset : Potential energy shift ! ptype : identifier for the particle types ! n : number of particles ! d : dimensionality of the vectors ! p : number of particle types ! ! Returns ! ------- ! vpot : the potential energy implicit none integer, intent(in) :: n, d, p double precision, dimension(n, d), target, intent(in) :: pos double precision, dimension(d), intent(in) :: box, ibox double precision, dimension(p, p), intent(in) :: lj3, lj4, offset, rcut2 integer, dimension(n), intent(in) :: ptype double precision, intent(out) :: vpot double precision :: rsq, r2inv, r6inv, dx, dy, dz double precision, dimension(:), pointer :: x, y, z integer :: i, j, itype, jtype vpot = 0.0D0 x => pos(1:n,1) y => pos(1:n,2) z => pos(1:n,3) do i=1,n-1 itype = ptype(i) + 1 !$omp parallel do private(jtype, dx, dy, dz, rsq, r2inv, r6inv) reduction (+:vpot) do j=i+1,n jtype = ptype(j) + 1 dx = x(i) - x(j) dy = y(i) - y(j) dz = z(i) - z(j) dx = pbc_dist(dx, box(1), ibox(1)) dy = pbc_dist(dy, box(2), ibox(2)) dz = pbc_dist(dz, box(3), ibox(3)) rsq = dx*dx + dy*dy + dz*dz if (rsq < rcut2(jtype, itype)) then r2inv = 1.0D0 / rsq r6inv = r2inv**3 vpot = vpot + r6inv * (lj3(jtype, itype) * r6inv - lj4(jtype, itype)) vpot = vpot - offset(jtype, itype) end if end do !$omp end parallel do end do end subroutine potential
Note that you will have to modify the flags in your Makefile accordingly, for instance, setting:
F2PY_FLAGS = --fcompiler=gfortran --f90flags='-fopenmp' -lgomp